Categorie archieven: Artikels

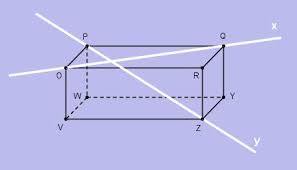
Ruimtemeetkunde

Geplaatst op door

In het zesde jaar van het MO wordt een cursus gegeven over ruimtemeetkunde. In dit artikel wordt een andere manier van benadering gegeven dan de meeste handboeken. We steunen op de theorie van de vectorruimten. We onderscheiden twee delen:

  1. Definitie van punten, vectoren, rechten en vlakken. We bespreken hun onderlinge ligging en evenwijdigheid en bewijzen een aantal stellingen daarrond. Dit vindt je hier.
  2. Via de definitie van een skalair product kunnen we ook spreken over loodrechte stand, afstanden en hoeken. De bespreking daarvan vindt je hier.

Niet-transitieve spelen

Geplaatst op door

In deze tekst onderzoeken we een eenvoudig dobbelspel: twee spelers hebben
een dobbelsteen, gooien deze, en wie het hoogst aantal ogen gooit wint. Er
blijken setjes dobbelstenen te bestaan waarbij geen van de stenen duidelijk
het sterkst is in dit spel. Het zijn namelijk niet-transitieve dobbelstenen.

Wat wil dit zeggen? Wel dobbelsteen B wint van A, dobbelsteen C wint van B … en dobbelsteen A wint van C. Dit doet denken aan het spel schaar-steen-papier, waar elke mogelijkheid sterker én zwakker is dan een andere. In deze tekst onderzoeken we welke strategie het beste is om de winstkans te maximaliseren.

Munten wegen

Geplaatst op door

weegschaal We hebben 13 muntstukken, waarvan er eentje vals is. De enige manier waarop de valse muntzich van de echte munten onderscheidt is door zijn gewicht. We beschikken over een weegschaal zonder gewichtsaanduiding. Wat is het minimum aantal wegingen dat we moeten doen om te bepalen welke munt vals is? Gegeven een aantal munten waarvan er eentje vals is en gegeven zijn k wegingen. Je weet dat het valse muntstuk zwaarder is dan een echt muntstuk. Wat is maximum aantal muntstukken waaruit je zeker het valse kan identificeren? Wil je hierop het antwoord kennen, lees dan volgende tekst.

Gehelen van Gauss

Geplaatst op door

Gehelen van Gauss zijn complexe getallen a+bi waarbij a en b gehelen getallen zijn. Je kan ze optellen en vermenigvuldigen. Zo vormen ze een interessante structuur : een commutatieve ring met eenheidselement. In deze tekst worden de basisbegrippen van de ringtheorie, aan de hand van de ring van de gehelen van Gauss, besproken. Zo bespreken we de eenheden, de priem elementen en de idealen van deze ring. Geen bewijzen , maar alle interessante begrippen komen aan bod. De lezer kan ze nadien zelf uitwerken. In onderstaande afbeelding vind je bijvoorbeeld alle priem elementen in het vlak van Gauss.

priem