Categorie archieven: Artikels

Stelling van Pythagoras

Geplaatst op door

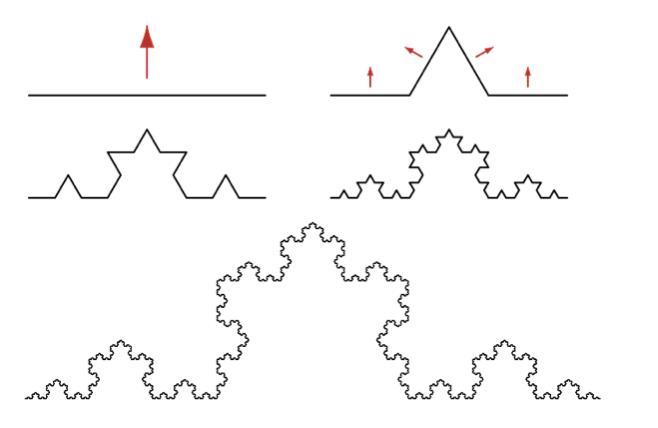
Deze tekst is gemaakt door Joran Deschagt, leerling van 6WEWI uit het H.Drievuldigheidscollege in Leuven.

 

    \[a^2+b^2=c^2\]

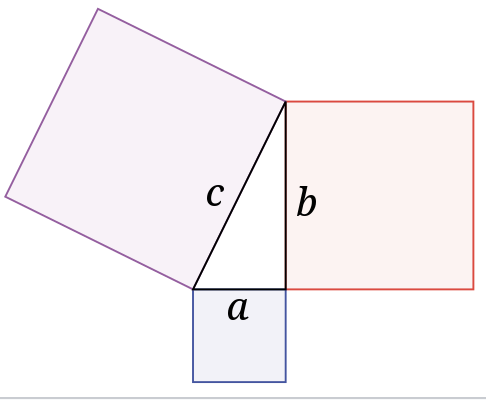
Iedereen kent de stelling dat in een rechthoekige driehoek de som van de kwadraten van de rechthoekszijden gelijk is aan het kwadraat van de schuine zijde. Wij kennen deze stelling als de stelling van Pythagoras. Maar deze stelling was al gekend bij de Soemeriërs en de Egyptenaren, lang voor Pythagoras.

Er zijn in feite heel  veel verschillende bewijzen voor de stelling van Pythagoras. Ook werden deze over heel de wereld ontworpen, van Azië tot Amerika. Er was er zelfs één van de Amerikaanse president, J. A. Garfield. We geven een kleine selectie:

Het oudste bewijs dat we hebben gevonden situeren we ergens tussen 1200 v.C. – 100v.C. in een oud Chinese leerboek Chou-Pei Suan Ching.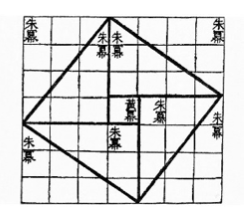

De zijde van het grote vierkant is a + b en de oppervlakte dus (a+b)^2. Hierbij zijn a en b de zijden van de rechthoekige driehoeken die getekend staan tussen het grote vierkant en het kleine vierkant. De zijde van het middelste vierkant is c. De oppervlakte van het grote vierkant is de som  van  de oppervlakten van de 4 rechthoeken en de oppervlakte van het kleine vierkant: (a+b)^2=4. \frac{ab}{2}+c^2. Hieruit volgt dan de stelling van Pythagoras.

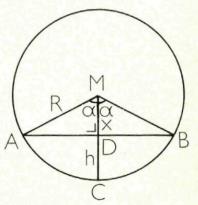
Het bewijs van president Garfield steunt op de oppervlakte van een trapezium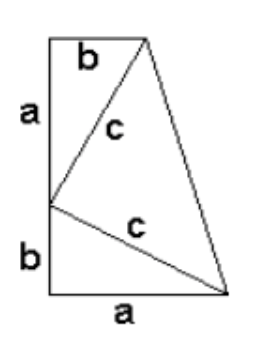

De oppervlakte van het trapezium is gelijk aan de som van de oppervlakten van de drie driehoeken, dus (a+b).\frac{a+b}{2}=\frac{ab}{2}+\frac{ab}{2}+\frac{c^2}{2}. Uitrekenen geeft ….de stelling van Pythagoras!

 

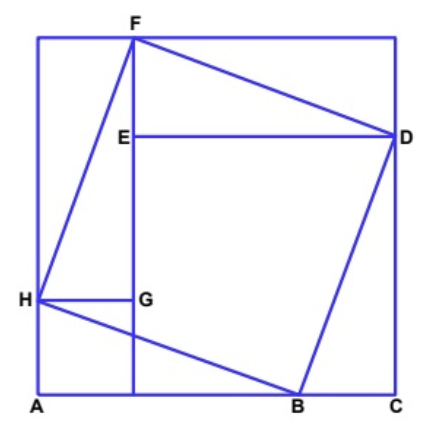
Een recenter bewijs komt van Xiaolin Zhong, professor aan het UCLA:

Draai de driehoeken ABH en BCD naar de driehoeken HGF en FED; Je ziet hier 4 keer die driehoek ‘rond’ het binnenste vierkant en 2 keer in dat binnenste vierkant. Het grootste vierkant heeft  een zijde van a + b en een oppervlakte gelijk aan (a+b)^2 en bestaat uit 4 rechthoeken en een vierkant met zijde EG. Het vierkant FDCH heeft oppervlakte c^2 en bestaat uit 4 driehoeken (die 2 rechthoeken vormen) en dat vierkant met zijde EG. Hieruit kan je het gewenste resultaat afleiden.

 

Dimensie

Geplaatst op door

Rechthoeken, driehoeken, cirkels,… zijn lange tijd de meest bestudeerde meetkundige figuren geweest. In realiteit komen deze figuren echter zelden voor. Als we eens een luchtfoto bekijken van de kustlijn van een willekeurig continent, dan blijkt die lijn niet meer zo ‘glad’ te zijn dan bij een rechthoek. Er is hier spraken van een fractaal.

De naam fractaal werd ingevoerd door Benoit Mandelbrot, die heeft willen aantonen dat de ons omgevende natuur rijk is aan fractals.

We willen het hier vooral hebben over de dimensie van dergelijke objecten. Dit artikel is geschreven door Luca Pignatti, leerling van 6WEWIe2 aan het H.Drievuldigheidscollege in Leuven.

We zoeken een  alternatieve definitie  voor de dimensie van een object. Daarvoor voeren we  een onderzoek naar dimensies op objecten waarvan we de dimensie reeds kennen. Een 1-dimensioneel lijnstuk, een 2-dimensioneel oppervlak en een 3-dimensionele kubus. Wanneer je elk voorwerp met een factor vergroot of verkleint bekom je hetzelfde voorwerp maar met een verschillende afmeting. Deze afmeting zou je ook kunnen beschouwen als de massa van het voorwerp, ook al is dit niet helemaal juist, een lijnstuk heeft geen massa. Het is wel een goede manier om het te visualiseren. Probeer je voor te stellen dat de voorwerpen uit metaal gemaakt zijn, metalen draad, metaalplaat en massief metaal. Een voorbeeld: verkleinen met factor ½

dimensie 1, lengte ½ , massa ½

dimensie 2, lengte ½, massa 1/4

dimensie 3, lengte ½, massa 1/8 

We vinden dat wanneer de lengte gehalveerd wordt,  de massa van het voorwerp met diezelfde factor tot de macht van de dimensie verheven wordt. Dit geldt niet enkel voor factor ½ maar voor elk ander reëel, positief getal. zo krijgen we de formule

    \[s^d=m\]

Hierbij is s de vergrotingsfactor, m de massa na de transformatie en  d  de dimensie .

Dit verband kan ons helpen met zoeken naar de dimensies van bepaalde fractalen, zoals de driehoek van Sierpinski. De driehoek van Sierpiński is een fractaal die werd ontdekt door de Poolse wiskundige Wacław Sierpiński. Uit een gelijkzijdige driehoek wordt de driehoek verwijderd die gevormd wordt door de middens van de drie zijden. Vervolgens wordt deze procedure herhaald in elk van de drie overgebleven driehoeken.

We zien dat wanneer we de zijde van de driehoek met factor ½ verkleinen dat de massa (oppervlakte)  van het voorwerp er na tot \frac{1}{3} van de massa ervoor is. Wanneer we onze formule invullen voor s=1/2 en m=1/3 vinden we (1/2)D = (1/3). De dimensie zou dan gelijk moeten zijn aan \log_23\approx 1,58496.

Laten we even kijken naar de kromme van Koch:

We vinden s=1/3, m=1/4 en dus is de dimensie van de Kochkromme gelijk aan \log_34\approx 1,26186.

De dimensie van onze fractals is dus niet langer een natuurlijk getal, maar wel een breuk! Iets tussen dimensie 1 en dimensie 2. 

 

 

De Rascal driehoek

Geplaatst op door

Als men, bij een IQ-test, zou vragen  om de driehoek te voltooien, dan krijg je meestal als antwoord:

Dit is de driehoek van Pascal. Vervolledigen kan via de formule

    \[u_{n,r}=u_{n-1,r-1}+u_{n,r-1}\]

Hierbij geeft r de rij weer en n de plaats op de rij. Zowel r als n starten bij de waarde 0.

Maar dit is niet het enige patroon dat je kan gebruiken. Wat denk je van volgend antwoord:

Het waren 3 middelbare school leerlingen,  Alif Anggoro, Eddy Liu, Angus Tulloch  uit de USA, Canada en Indonesië die dit verband beschreven met de formule

    \[u_{n,r}=n(r-n)+1\]

Je kan ook gebruik maken van de diagonaalformule :

Het getal op zuid is ( oost x west +1 ) : noord. Bij de driehoek van Pascal was zuid = oost + west.

Eigenaardig genoeg is elk element in de Rascal driehoek een natuurlijk getal! Net zoals bij de driehoek van Pascal kan je ook hier een paar mooie patronen terugvinden. Kijk maar naar de diagonalen van de Rascal driehoek

Wiskunde en wijn

Geplaatst op door

Een wijnroeier is iemand die met een peilstok ( wijnroede genaamd) de hoeveelheid wijn in een vat meet.  Het beroep van wijnroeier kwam in Europa voor tot in de negentiende eeuw.

Een gelijkaardig probleem bestaat erin met een peilstok de hoeveelheid mazout in een tank te meten. Laten we veronderstellen dat het vat cilindrisch is. Het heeft de straal R en de lengte l. We zoeken nu een relatie tussen de inhoud I van de nog aanwezige wijn of olie en de hoogte h, waarover de lat door de vloeistof bevochtigd wordt.

We berekenen daartoe eerst de oppervlakte O van het cirkelsegment ACB.  Dit is het verschil van de oppervlakten van de sector MACB en  de driehoek MAB.

Door gebruik te maken van gekende formules vonden we dat deze oppervlakte gelijk is aan \alpha R^2-\frac{1}{2}R^2\sin 2\alpha.
Bijgevolg is de inhoud van de aanwezige vloeistof gelijk aan

    \[I=\frac{1}{2}lR^2(2\alpha-\sin 2\alpha)\]

Het verband tussen I en h is moeilijk uit te drukken. We weten wel dat h=R(1-\cos \alpha). We gaan een paar h waarden nemen en daarvoor \alpha en I berekenen en dat in grafiek zetten of een meetlat maken.

Het was J.Kepler, die naar aanleiding van het bezoek van een wijnroeier, zijn Nova stereometria doliorum (1615) en  Messekunst Archimedis (1616) schreef waarin hij de inhoud van bepaalde omwentelingslichamen bepaalde ( zonder integraalrekening!) en de praktische  toepassing ervan bij het wijnroeien.

Nagels en draad

Geplaatst op door

Een aardig knutselwerkje: klop wat nagels in een plank en verbind deze met wat draad en probeer alzo een mooie figuur te bekomen. In volgend artikel kan je lezen over een wiskundige versie van deze activiteit. Permutaties en ideeën uit d etheorie der groepen worden hier geïllustreerd.