In een vorig artikel bespraken we Hamming-codes. De Hamming (7,4) code codeert een 4-bits boodschap  naar een 7-bits codewoord
naar een 7-bits codewoord  , door drie even pariteitsbits toe te voegen:
, door drie even pariteitsbits toe te voegen:
![Rendered by QuickLaTeX.com \[p_5=p_1+p_2+p_4\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-17b6cbed6ea8aa43eb3e65496237092d_l3.png?media=1678572382)
![Rendered by QuickLaTeX.com \[p_6=p_1+p_3+p_4\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-362a9eba73239f060769c7a05e59dc19_l3.png?media=1678572382)
![Rendered by QuickLaTeX.com \[p_7=p_2+p_3+p_4\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-25806dc88c151553683150a2338cc8ad_l3.png?media=1678572382)
De vergelijkingen dienen modulo 2 bekeken te worden.
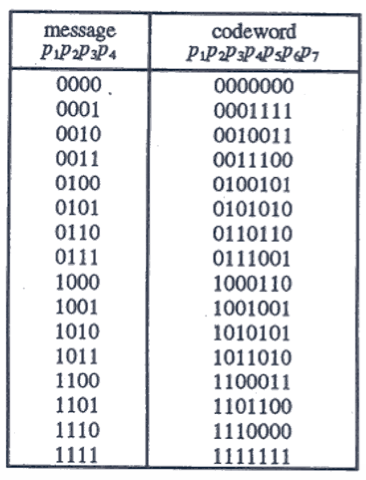
Dit zijn de 16 mogelijke codewoorden. Om 0100 te zenden, stuur je het codewoord 0100101 door. Als er 1 transmissiefout op zit en je ontvangt 0101101, dan kan de ontvanger de fout vinden door het dichts bijzijnde codewoord te gebruiken. Inderdaad, 0100101 is het enige codewoord dat in slechts 1 positie verschilt van 0101101.
Neem nu even de eerste zes bits van een codewoord en verdeel ze als 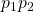 ,
, en
en 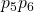 . Gebruik nu het eindige veld met 4 elementen, gedefinieerd door volgende bewerkingen:
. Gebruik nu het eindige veld met 4 elementen, gedefinieerd door volgende bewerkingen: 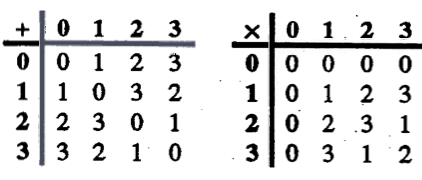
Neem nu terug het codewoord 0100101. De punten 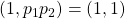 ,
,  en
en  blijken alle drie op de rechte y=2x+3 te liggen. Reken na met bovenstaande bewerkingstabellen. Deze eigenschap kan gebruikt worden bij het decoderen. Veronderstel dat het ontvangen codewoord 0101101 is. Met de zes eerste bits vormen we, zoals hierboven beschreven drie punten
blijken alle drie op de rechte y=2x+3 te liggen. Reken na met bovenstaande bewerkingstabellen. Deze eigenschap kan gebruikt worden bij het decoderen. Veronderstel dat het ontvangen codewoord 0101101 is. Met de zes eerste bits vormen we, zoals hierboven beschreven drie punten  en
en  . De rechte door A en B bevat C niet.Omdat de Hamming code 1 fout kan detecteren, veronderstellen we dat 1 van de punten fout is. De oorspronkelijke rechte is dus ofwel
. De rechte door A en B bevat C niet.Omdat de Hamming code 1 fout kan detecteren, veronderstellen we dat 1 van de punten fout is. De oorspronkelijke rechte is dus ofwel 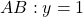 ,
, 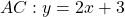 of
of  . Dan zouden de zes eerste bits van het originele codewoord 010101,010010 of 110110 moeten zijn. Onder deze drie mogelijkheden voldoet enkel 010010 aan
. Dan zouden de zes eerste bits van het originele codewoord 010101,010010 of 110110 moeten zijn. Onder deze drie mogelijkheden voldoet enkel 010010 aan  mod 2. Bijgevolg decoderen we de ontvangen boodschap 0101101 als 0100101 en was de oorspronkelijke boodschap 0100.
mod 2. Bijgevolg decoderen we de ontvangen boodschap 0101101 als 0100101 en was de oorspronkelijke boodschap 0100.
Deze proceduren lijkt erg complex. Ze kan echter veralgemeend worden om meer fouten verbeterende codes te construeren, door gebruik te maken van veeltermen in plaats van rechten.
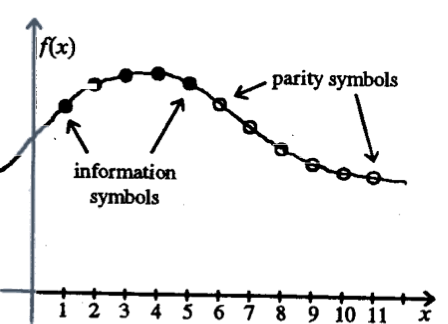
Het idee om dergelijke veetermen te gebruiken werd het eerst naar voren gebracht door Reed en Solomon in 1960.

 In deze tekst onderzoeken welke we getallen er construeerbaar zijn met de klassieke constructieapparaten, passer en liniaal. Verder bestuderen we ook de structuur van de verzameling van alle construeerbare getallen. We komen zo tot een modern algebraïsch bewijs van de onmogelijkheid om met passer en liniaal een kubus te verdubbelen. Dit is een welbekend probleem uit de oude Griekse meetkunde. Zo zien we dat algebra en meetkunde enerzijds en oude en moderne wiskunde anderzijds erg nauw samenlopen.
In deze tekst onderzoeken welke we getallen er construeerbaar zijn met de klassieke constructieapparaten, passer en liniaal. Verder bestuderen we ook de structuur van de verzameling van alle construeerbare getallen. We komen zo tot een modern algebraïsch bewijs van de onmogelijkheid om met passer en liniaal een kubus te verdubbelen. Dit is een welbekend probleem uit de oude Griekse meetkunde. Zo zien we dat algebra en meetkunde enerzijds en oude en moderne wiskunde anderzijds erg nauw samenlopen.