 Vaak bestaat een probleem erin aan te tonen dat een bepaalde
eigenschap geldt voor elk natuurlijk getal.
Als je wilt weten of iets waar is voor alle natuurlijke
getallen n (dus voor n = 1, 2, 3, . . .), kun je ze niet
allemaal afgaan: daar zou je oneindig lang mee bezig zijn.
Inductie is eigenlijk een verzameling van bewijstechnieken
die de waarheid van een stelling voor alle elementen van een
verzameling aantonen door gebruik te maken van de onderliggende
structuur van de verzameling.
Om de geldigheid te bewijzen van een uitspraak van de vorm
" Voor ieder natuurlijk getal
Vaak bestaat een probleem erin aan te tonen dat een bepaalde
eigenschap geldt voor elk natuurlijk getal.
Als je wilt weten of iets waar is voor alle natuurlijke
getallen n (dus voor n = 1, 2, 3, . . .), kun je ze niet
allemaal afgaan: daar zou je oneindig lang mee bezig zijn.
Inductie is eigenlijk een verzameling van bewijstechnieken
die de waarheid van een stelling voor alle elementen van een
verzameling aantonen door gebruik te maken van de onderliggende
structuur van de verzameling.
Om de geldigheid te bewijzen van een uitspraak van de vorm
" Voor ieder natuurlijk getal 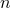 geldt
geldt 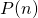 ",
waarbij
",
waarbij 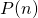 staat voor een bewering (propositie) waarin
staat voor een bewering (propositie) waarin 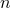 voorkomt, maakt men vaak gebruik van deze methode.
Lees meer hierover in volgend artikel, waar een paar
voorbeelden worden uitgewerkt en waar ook een heleboel opgaven staan.
voorkomt, maakt men vaak gebruik van deze methode.
Lees meer hierover in volgend artikel, waar een paar
voorbeelden worden uitgewerkt en waar ook een heleboel opgaven staan.
Vaak bestaat een probleem erin aan te tonen dat een bepaalde eigenschap geldt voor elk natuurlijk getal. Als je wilt weten of iets waar is voor alle natuurlijke getallen n (dus voor n = 1, 2, 3, . . .), kun je ze niet allemaal afgaan: daar zou je oneindig lang mee bezig zijn. Inductie is eigenlijk een verzameling van bewijstechnieken die de waarheid van een stelling voor alle elementen van een verzameling aantonen door gebruik te maken van de onderliggende structuur van de verzameling. Om de geldigheid te bewijzen van een uitspraak van de vorm " Voor ieder natuurlijk getal
geldt
", waarbij
staat voor een bewering (propositie) waarin
voorkomt, maakt men vaak gebruik van deze methode. Lees meer hierover in volgend artikel, waar een paar voorbeelden worden uitgewerkt en waar ook een heleboel opgaven staan.
