In 1815 werd Augusta, kortweg Ada, geboren als dochter van de bekende Engelse dichter Lord Byron en barones Milbanke. Ada’s moeder zou haar opvoeden tot wiskundige en onderzoeker. De reden hiervoor was dat ze bang was dat Ada anders net als haar vader zou eindigen als dichter.
Via de Schotse Mary Sommerville, een schrijfster van wetenschappelijke boeken, kwam Ada op haar 17de in contact met Charles Babbage( 1791-1871). Omdat deze laatste zich ergerde aan de fouten in vele astronomietabellen, bedacht hij zijn Difference Engine, een door stoom aangedreven mechanische machine die deze berekeningen automatisch kon uitvoeren. De machine steunde op de methode van eindige verschillen ontwikkeld door de wiskundige Gaspard de Prony (1755-1839), waardoor ze niet moest kunnen vermenigvuldigen of delen, wat mechanisch moeilijk uit te voeren was.
Ada, inmiddels getrouwd met Lord William King, graaf van Lovelace, begreep onmiddellijk het potentieel van de programmeerbare machine, eigenlijk de voorloper van onze huidige computers.
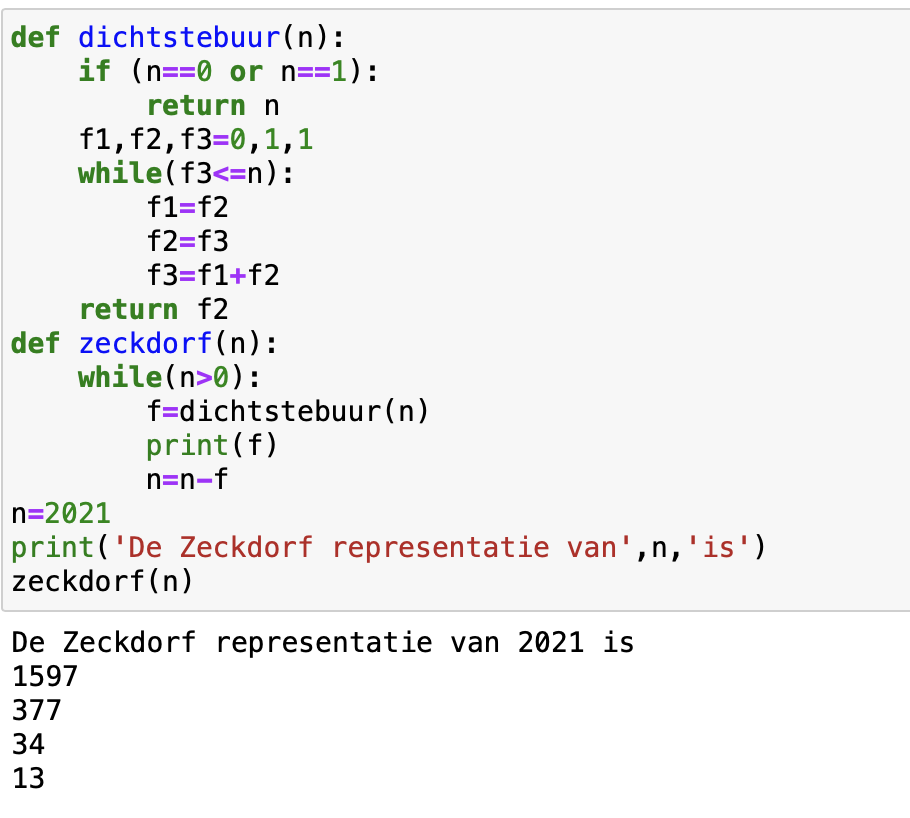
Lovelace kon niet zo maar onder haar eigen naam een artikel publiceren. Daarom vertaalde ze een samenvatting van het artikel Notions sur la Machine Analytique ( van Luigi Menabrea) uit het Frans naar het Engels. Babbage stelde voor dat zij dit met haar eigen aantekeningen zou uitbreiden tot een artikel – wat de oorspronkelijke tekst drie keer zo lang maakte. Dit artikel werd gepubliceerd in 1843; In een appendix stond uitgeschreven hoe de machine een recursieve wiskundige berekening kon uitvoeren om de rij van Bernouilli-getallen te berekenen. Babbage had die nodig om zijn astronomische functies beter te benaderen. Dit uitgeschreven plan wordt nu beschouwd als het eerste computerprogramma.
Ada Lovelace overleed op 36-jarige leeftijd aan bloedingen ten gevolge van een behandeling tegen baarmoederkanker.
De programmeertaal Ada, in 1979 ontwikkeld in opdracht van het Amerikaanse Ministerie van Defensie, is naar haar vernoemd.

![]()
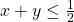 .
.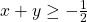 .
. . Is echter x+y<0, dan verkrijgen we
. Is echter x+y<0, dan verkrijgen we 
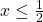 . Is daarentegen x+y<0, dan krijgen we
. Is daarentegen x+y<0, dan krijgen we