Auteur archieven: admin

Omzetting mijlen naar kilometer

Geplaatst op door

1 mijl( = 1 mi ) is 1,609344 km, wat dicht bij het gulden getal \varphi =1,618 ligt. De waarde van \varphi wordt benaderd door de verhouding van twee opeenvolgende getallen in de rij van Fibonacci. Daarom kan je voor de omzetting van mijlen naar kilometer en omgekeerd gebruik maken van opeenvolgende Fibonacci getallen, met vrij grote nauwkeurigheid.

Priemtweelingen

Geplaatst op door

Een paar opeenvolgende priemgetallen waarvan de afstand 2 is, noemen we een priemtweelingen. Buiten de eerste priemtweelingen 3-5 vinden we bijvoorbeeld ook 5-7, 11-13, 17-19,… Ze ontstaan allemaal (behalve 3-5), door vertrekkend van 5-7, een translatie uit te voeren over 6 eenheden. Dit is logisch want een priemgetal is altijd van de vorm 6k+1 of 6k-1. 

Een Python programma om alle priemtweelingen kleiner dan 1000 te bepalen:
De output:

Een paar ‘leuke ‘ eigenschappen, die zeer eenvoudig te bewijzen zijn:

  • Een priemtweelingen heeft een symmetriemidden dat steeds een 6-voud is.
  • De som van twee elementen van een priemtweelingen is steeds een 12-voud.
  • De afstand voor de overeenkomstige elementen van twee priemtweelingen is steeds een 6-voud.
  • De afstand van het grootste getal van de kleinste priemtweeling tot het kleinste getal van de grootste priemtweelingen is een 6-voud min 1.
  • Er bestaat geen grootste priemtweeling.

                                  

Opgave 34: Een integraal…

Geplaatst op door

Bereken A=\int_0^{\frac{\pi}{4}} ln(1+tan x) dx

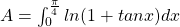
  • Gewone methoden werken hier niet.
  • Als een functie f gedefinieerd is op \left[a,b\right] dan kan je de functie spiegelen rond de middelloodlijn van dit lijnstuk en bekom je de functie g(x)=f(a+b-x).
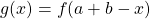  • Uit de definitie van de bepaalde integraal volgt dan dat \int_a^bf(x) dx=\int_a^b g(x) dx.
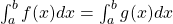  • Passen we dit toe op de opgave , dan krijgen we: A=\int _0^{\frac{\pi}{4}} ln(1+tan(\frac{\pi}{4}-x)) dx.
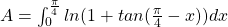  • Nu is tan(\frac{\pi}{4}-x)=\frac{1-tan x}{1+tan x}.
  • Zodat A=\int _0^{\frac{\pi}{4}} ln\Big( \frac{2}{1+ tan x}\Big) dx.
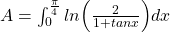  • Gebruikmakend van de rekenregels voor logaritmen, volgt hieruit dat A=\int _0^{\frac{\pi}{4}} ln(2) dx -A.
  • Bijgevolg is A=\frac{\pi}{8} ln(2).

Rationale getallen

Geplaatst op door

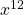Is het juist dat, indien x^7 en x^{12} rationaal zijn, x eveneens rationaal is?

We weten dat de vermenigvuldiging en de delig door een getal, verschillend van 0, inwendige bewerkingen zijn in \mathbb{Q}.  Dus als x^{12} en x^7 rationaal zijn, dan is hun quotiënt x^5 dat ook . Maar dan is het quotiënt van x^7 en x^5, en dat is x^2, ook een rationaal getal. Als x^2 rationaal is, dan ook (x^2)^3=x^6. Tenslotte volgt uit het feit dat x^6 en x^5 allebei rationaal zijn dat hun quotiënt x dat ook is.Het antwoord op de gestelde vraag is dus bevestigend.

We kunnen dit ook anders oplossen: We zoeken eigenlijk twee getallen a en b zodat (x^{12})^a:(x^7)^b=x, waarbij a en b gehele getallen zijn. Maar dan moet

    \[12a-7b=1\]

Dit is een Diophantische vergelijking en omdat de grootste gemene deler van 12 en 7 gelijk is aan 1, heeft deze vergelijking oneindig veel oplossingen. De meest eenvoudige is a=3 en b=5. Dit geeft ons in één keer ook de mogelijkheid het probleem te veralgemenen. Als we in de opgave werken met bijvoorbeeld x^9 en x^{12}, dan klopt het niet meer: de Diophantische vergelijking 12a-9b=1 heeft immers geen oplossingen omdat de grootste gemene deler van a en b gelijk is aan 3.

Computationeel denken

Geplaatst op door
Computationeel denken is een denkmethode waarbij je alles wat je doet, omschrijft in kleine deelstappen zodat je een opdeling krijgt van de op te lossen ‘probleempjes’. Het is een individueel proces. Elke leerling werkt vanuit andere deelvragen. Hoe jonger je leerlingen zijn, hoe meer gelijklopend die deelvragen of stappen zullen zijn.

Er zijn met computationeel denken altijd meerdere mogelijke  werkwijzen. De oplossing binnen wiskunde zal hetzelfde zijn voor de hele klas, maar elke leerling kan een eigen strategie kiezen of bedenken om tot die oplossing te geraken. Vanaf dat een kind praat, stelt het zelf alles in vraag “Waarom?”. Hoe jonger het kind, hoe kleiner we de deelstappen maken.”

Eerst wordt er een overzicht gegeven van het eindproduct ‘het grote probleem’ om vervolgens stap voor stap het probleem op te lossen. Er wordt stap voor stap, blok per blok gebouwd om tot het geheel te komen. Eigenlijk is dat computationeel denken. Oudere leerlingen zijn zelf in staat om te beslissen welke vragen ze zichzelf moeten stellen om tot het eindproduct te komen.


Wiskunde is het meest logische vak om computationeel denken aan te leren. Als heuristiek wordt een probleem opgelost door het stellen van deelvragen, denk aan het algoritme: gegeven, gevraagd, oplossing. Probleemoplossend denken is eigenlijk hetzelfde basisprincipe als computationeel denken. Het inzichtelijk leren of het leren door zichzelf vragen te stellen, stelt de leerling in staat inzicht te krijgen in het grote geheel. 

De Amerikaanse onderzoekster Jeannette Wing introduceerde in 2006 het begrip computationeel denken als volgt:

“Computational thinking is reformulating a seemingly difficult problem into one we know how to solve, perhaps by reduction, embedding, transformation or simulation.”

Computationeel denken is daarom, volgens haar,  een basisvaardigheid, die iedereen zou moeten beheersen, naast lezen, rekenen en schrijven.