Auteur archieven: admin
Soemerië : vroeg-dynastieke periode (2900-2334 V.C.)
In het vroege derde millennium kreeg Uruk concurrentie van ondermeer Kish, gelegen in het noorden van Soemer. De steden in het zuiden werden herhaaldelijk getroffen door overstromingen. Deze vormden trouwens de inspiratie van veel zondvloed verhalen.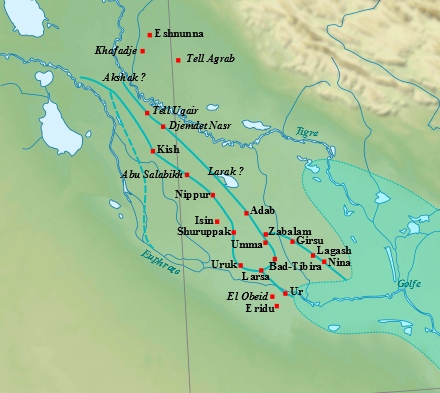
in deze periode ontstond een nieuwe klasse van grootgrondbezitters. Net als de tempels bezaten ze veel landbouwgrond en hadden ze veel mensen in dienst. men noemden hen lugals( grote mannen).
Omdat hun bedienden al het werk deden, hadden de lugals tijd om zich met andere dingen ( zoals oorlog voeren) bezig te houden. Omdat de bevolking fors toenam, was het onvermijdelijk dat er meer en meer grensconflicten werden uitgevochten op het slagveld. Elke lugal nam een een aantal van zijn mannen mee en soms werd één van hen als een soort opperbevelhebber aangeduid. De legendarische Gilgamesh van Uruk was waarschijnlijk één van hen.
In de loop van het derde millennium bleef Soemer verdeeld onder verschillende stadstaten . De lugals waren weinig meer dan opperbevelhebbers. De hogepriester bleef het ‘staatshoofd’. Ondanks hun gebrek aan politieke eenheid groeide wel het besef van culturele eenheid: de beschermgoden van de verschillende stadstaten kregen een vaste plaats in het pantheon. Enlil, die vereerd werd in Nippur, werd aangewezen als oppergod.
De Soemerische koningslijst, die veel later werd opgesteld, is een belangrijke bron van informatie over deze tijd. Vermelden we ondermeer volgende heersers:
- Enmebaragesi van Kisj, die vocht tegen Elam.

- Urakagina van Lagash:hij voerde veel hervormingen in en presteerde zich als een rentmeester die in de naam van de goden het bewind voerde over de landgoederen. Dit idee van goed rentmeesterschap was zeer belangrijk in de Soemerische traditie.

- Meshannepada, vorst van Ur, stichtte de eerste dynastie van Ur. De koningsgraven zijn een mooi bewijs hoe welvarend Ur wel was.

Er waren zeer heel intensieve handelsactiviteiten met streken buiten hun grondgebied( Mari, Terqa, Ebla, Assur, Tell Brak) - Eannatum van Lagash. bekend is zijn overwinning op Umma, herdacht op de gierenstèle.

- Lugal-Zagesi van Umma werd de eerst absolute heerser over de vruchtbare Halvemaan, met een grondgebied dat de hele Mesopotamische vlakte besloeg. Alhoewel die zeggenschap niet echt reëel was, vermits het merendeel van de stadstaten gehecht was aan hun onafhankelijkheid.
Geleidelijk aan ontstond er naast de tempel ook een ander gebouw: het paleis. tempel en paleis vormden een tweekoppige macht die de Soemerische geschiedenis lang zou kenmerken.
Nootje 29
Gegeven is een veelterm waarvan de coëfficiënten natuurlijke getallen zijn. Hoe kan je met zo weinig mogelijk evaluaties met natuurlijke getallen( berekenen van een getalwaarde) de coëfficiënten bepalen? Probeer eerst eens als alle coëfficiënten kleiner zijn dan 10.
Derdegraads vergelijkingen: vervolg.
In een vorig artikel hebben we de formules van Cardano besproken voor het oplossen van een willekeurige vergelijking van graad 3. Maar wat heeft de symmetrische groep van orde 6,![]() hier mee te maken? En wat is de discriminant van zo een vergelijking? Is dat dan een veralgemening van de discriminant van een vergelijking van graad 2? Wil je hierover meer weten , lees dat dit vervolgartikel.
hier mee te maken? En wat is de discriminant van zo een vergelijking? Is dat dan een veralgemening van de discriminant van een vergelijking van graad 2? Wil je hierover meer weten , lees dat dit vervolgartikel.
Opgave 36
Wanneer deelt een natuurlijk getal n de uitdrukking ![]() voor een natuurlijke k?
voor een natuurlijke k?


