Suezcrisis

Geplaatst op 4 september 2022 door admin

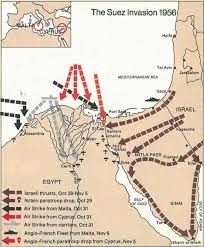
Het Suez kanaal is 193 km lang kanaal en verbindt de Middellandse zee met de Rode zee. Het is zo een verbinding tussen de Indische oceaan en de atlantische oceaan. Het is zeer belangrijk voor de scheepvaart van Azië naar Europa en het westen. Tot hiervoor moesten de schepen helemaal rond Afrika varen.

De Brits-Franse aandeelhouders streken sinds 1882 haast alle winsten op. Maar op 26 juli 1956 legde Gamal Abdel Nasser beslag op het Suezkanaal.

De beslissing viel omdat hij geen steun had gekregen van het Verenigd Koninkrijk voor de bouw van de Aswan-dam. Frankrijk en Engeland zagen hun bron van inkomsten verdwijnen en kwamen tot het besef dat de doorgang niet meer verzekerd was en dat de olietoevoer bedreigd werd. Bovendien veroordeelde Nasser de koloniale politiek van Engeland in het Midden-Oosten, ten voordele van Israël?

Terwijl een conferentie, zonder Egypte, startte in Londen, spanden Frankrijk,Engeland en Israël samen voor een aanval op Egypte. Israël spande samen met de Europese machten, uit woede om de Egyptische aanvallen aan de grens met Sinaï. Bovendien had Nasser de golf van Akaba geblokkeerd zodat Israël vanuit de Rode zee onbereikbaar was geworden. Zo ontstond Operation Musketier om het Suezkanaal terug in handen te krijgen. Op 29 oktober 1956 viel Israël de Gazastrook en het Sinaï-schiereiland binnen en begon zijn opmars naar de kanaalzone. Kort daarop begonnen Engeland en Frankrijk vanuit Malta, Cyprus en vliegdekschepen doelen in Egypte te bombarderen. Nasser reageerde door verschillende schepen te laten zinken en zo de waterweg te blokkeren.

De Verenigde staten waren misnoegd dat ze niet waren ingelicht en waren bevreesd dat Egypte helemaal in et communistische kamp zou terecht komen. Ze hadden al een wapendeal met Rusland gesloten! Daarom kwam Eisenhouwer tussenbeiden en oefende druk uit op de bondgenoten om een eind te maken aan de militaire actie. Hij dreigde de economische hulp, die na WO2 geboden werd, op te schorten.

Ook Rusland was woedend om wat een ‘koloniale invasie’ werd genoemd en Chroesjtsjov liet Nasser weten dat rechtstreeks hulp weliswaar onmogelijk was maar hij uitte wel bedreigingen om raketten af te vuren op Londen en Parijs. China, voor wie de doorgang héél belangrijk was, steunde Nasser eveneens.

Na een staakt het vuren, uitgevaardigd door de VN, begon de terugtrekking van de troepen. VN-troepen namen het van en over. Het Suezkanaal was voortaan Egyptisch, de politieke en financiële geschillen werden beslecht en de Aswan-dam kwam er met de hulp van Rusland.

Het fiasco van Operation Musketier, gedwarsboomd door de VS, Rusland en China, betekende het einde van het Europese imperialisme en was het begin van een nieuwe wereldorde.

Derdegraads vergelijkingen

Geplaatst op 1 september 2022 door admin

derdegraadsvergelijkingen

Een algemene tweedegraads vergelijking $ax^2+bx+c=0$ kan worden opgelost met de formule

$x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}$

We vragen ons af of er voor een willekeurige derdegraads vergelijking $ax^3+bx^2+cx+d=0$ , met $a\neq0$ , ook een algemene oplossingsmethode bestaat. We weten wel al zeker dat elke derdegraads vergelijking minstens 1 re\”ele oplossing heeft. Dit in tegenstelling tot de tweedegraads vergelijkingen waar niet elke vergelijking een re\”ele oplossing heeft.

Lees hier verder.

Overdekkingen van het vlak

Geplaatst op 27 augustus 2022 door admin

We gaan op zoek naar regelmatige bedekkingen van het vlak: dit zijn bedekkingen met regelmatige n-hoeken met alle dezelfde lengte als zijde. Het vlak is dan de unie van al die veelhoeken en de doorsnede van twee veelhoeken is ledig, ofwel een punt ofwel een zijde. We eisen ook dat de hoekpunten gelijkwaardig zijn, dus dat in een punt steeds dezelfde veelhoeken in dezelfde aantallen en in dezelfde volgorde voorkomen. Noteren we met $q$ het aantal verschillende veelhoeken in een bepaald knooppunt.

De waarde van een hoek van een regelmatige n-hoek is

$\frac{n-2}{n}180^{\circ}$

Neem eerst het geval $q=1$ . Noteer met m het aantal veelhoeken in een knooppunt. Dan moet $m.\frac{n-2}{n}180^{\circ}=360^{\circ}$ . Hieruit volgt dat $m(n-2)=2n$ of $(m-2)(n-2)=4$ . Hierbij zijn uiteraard m en n natuurlijke getallen. De enige oplossingen zijn:

$(m,n)=(6,3), (m,n)=(3,6), (m,n)=(4,4)$

Dus drie zeshoeken, zes driehoeken of vier vierkanten.

Neem nu $q=2$ ( we spreken dan van Archimedische vlakvullingen) en stel dat er a regelmatige m-hoeken en b regelmatige n-hoeken samenkomen, dan moet $a.\frac{m-2}{m}180^{\circ}+b.\frac{n-2}{n}180^{\circ}=360^{\circ}$ of

$a+b=2(\frac{a}{m}+\frac{b}{n}+1)$

Omdat $\frac{a}{m}+\frac{b}{n}>0$ zal $a+b\geq3$ . Omdat de klenst mogelijke hoek van een regelmatige veelhoek $60^{\circ}$ is, zal $a+b\leq 6$ . Bijgevolg geldt:

$3 \leq a+b \leq 6$

Geval 1: $a=1$ en $b=2$ , dan is $n=\frac{4m}{m-2}$ en zijn de enige natuurlijke oplossingen: $(m,n)=(3,12)$ en $(m,n)=(4,8)$ . De oplossing $(m,n)=(6,6)$ hebben we al en $(m,n)=(10,5)$ geeft geen regelmatige overdekking. De twee oplossingen geven we volgende typering: $3,12^2$ ( 1 driehoek en 2 twaalfhoeken) en $4,8^2$ (1 vierkant en 2 achthoeken).

Geval 2: $a=1$ en $b=3$ , dan is $n=\frac{3m}{3m-2}$ en is de enige natuurlijke oplossing: $(m,n)=(4,4)$ en die hebben we al gehad bij $q=1$ .

Geval 3: $a=1$ en $b=4$ , dan is $n=\frac{8m}{m-2}$ en zijn de enige natuurlijke oplossingen: $(m,n)=(6,3)$ . Typering: $6,3^4$ ( een zeshoek en 4 driehoeken)Geval 4: $a=2$ en $b=2$ , dan is $n=\frac{2m}{m-2}$ en zijn de enige natuurlijke oplossingen: $(m,n)=(3,6)$ , $(m,n)=(4,4)$ en $(m,n)=(6,3)$ . De oplossing $(m,n)=(4,4)$ hebben we al. Bovendien geven $(6,3)$ en $(3,6)$ dezelfde oplossing.Rest nog het geval $6^2,3^2$ (2 zeshoeken en 2 driehoeken).

Geval 5: $a=2$ en $b=3$ , dan is $n=\frac{6m}{3m-4}$ en is de enige natuurlijke oplossing: $(m,n)=(4,3)$ . Type $4^2,3^3$ ( twee vierkanten en drie driehoeken). We verfijnen de typering: links de overdekking $(3,3,3,4,4)$ en rechts $(3,3,4,3,4)$ .

Neem nu $q=3$ en stel dat er a regelmatige m-hoeken, b regelmatige n-hoeken en c regelmatige p-hoeken samenkomen, dan moet $a.\frac{m-2}{m}180^{\circ}+b.\frac{n-2}{n}180^{\circ}+c.\frac{p-2}{p}180^{\circ}=360^{\circ}$ of

$a+b+c=2(\frac{a}{m}+\frac{b}{n}+\frac{c}{p}+1)$

Waarbij $3\leq a+b+c<6$ zodat voor $(aub,c)$ volgende mogelijkheden moeten worden onderzocht: $(1,1,1),(2,1,1),3,1,1)$ en $(2,2,1)$ .

Geval 1: $(a,b,c)=(1,1,1)$ . Dan is $p=\frac{2mn}{mn-2m-2n}$ . Onderzoek van verschillende mogelijkheden geeft $(m,n,p)=(5,10,5),(5,20,4),(6,12,4),\\(8,8,4),(12,12,3),(15,10,3),(18,9,3),(24,8,3),(42,7,3)$ . Enkel $(m,n,p)=(6,12,4)$ levert een nieuwe bestaande overdekking. We krijgen een zeshoek, een twaalfhoek en een vierkant in elk knooppunt.

Geval 2: $(a,b,c)=(2,1,1)$ . Enkel $(m,n,p)=(4,6,3)$ levert een nieuwe bestaande overdekking. We krijgen twee vierkanten , een zeshoek en een driehoek in elk knooppunt. Geval 3: $(a,b,c)=(3,1,1)$ . Deze combinatie levert geen nieuwe oplossingen.

Geval 4: $(a,b,c)=(2,2,1)$ . Deze combinatie levert geen nieuwe oplossingen.

Situaties met $q=4,5$ of $6$ kunnen niet voorkomen want $60+90+108+120=378>360$ .

Fascisme

Geplaatst op 19 augustus 2022 door admin

Op 23 maart 1919 maakt Benito Mussolini in Milaan bekend dat hij een nieuwe beweging wil oprichten: de Fasci Italiani de Combattimento.

De naam Fasci verwijst naar de Romeinse fasces, symbool voor macht, samenhorigheid en eenheid.

De aanleiding hiertoe is de anarchie waarin Italië verkeert na het einde van WO1. Op 6 juni maakt Mussolini zijn doelen bekend in zijn krant Il Popolo d’Italia : een achturige werkdag, betere sociale voorzieningen, schoolplicht, confiscatie van kerkelijke eigendommen, verdeling van de grond onder veteranen, verdrijving van de elite en vooral een krachtige buitenlandse politiek.

Zijn aanhang groeit snel en overal ontstaan knokploegen die eigenhandig Mussolini willen helpen. Een golf van geweld overspoelt Italië en Mussolini beweert dat hij de enige leider ( duce) is die de orde kan herstellen en Italië weer groot kan maken.

In mei 1925 neemt hij deel aan de verkiezingen en haalt 35 van de 275 zetels, een reden om 5 maand later zijn beweging om te vormen tot een politieke partij: de Partite Nazionale Fascista (PNF). Een jaar later marcheert hij met 25000 volgelingen naar Rome. Koning Victor Emmanuel 3 wil verder geweld en een eventuele burgeroorlog voorkomen, en vraagt Mussolini een nieuwe regering te vormen onder diens leiding.

Construeerbare getallen

Geplaatst op 17 augustus 2022 door admin

In deze tekst onderzoeken welke we getallen er construeerbaar zijn met de klassieke constructieapparaten, passer en liniaal. Verder bestuderen we ook de structuur van de verzameling van alle construeerbare getallen. We komen zo tot een modern algebraïsch bewijs van de onmogelijkheid om met passer en liniaal een kubus te verdubbelen. Dit is een welbekend probleem uit de oude Griekse meetkunde. Zo zien we dat algebra en meetkunde enerzijds en oude en moderne wiskunde anderzijds erg nauw samenlopen.

Wiskunde is leuk

Auteur archieven: admin

Suezcrisis

Derdegraads vergelijkingen

Overdekkingen van het vlak

Fascisme

Construeerbare getallen