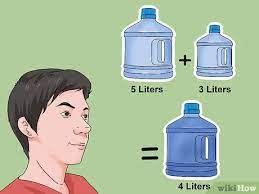
In dit artikel bespreken we problemen waarin men beschikt over 2 lege kannen, zonder maatstreepjes. Verder is er een kraan waarmee men de kannen kan vullen en een gootsteen waarin men de kannen kan leeggieten. We aanvaarden volgende handelingen : Een kan volledig leeggieten, een kan helemaal vullen met de kraan, water van de ene kan overhevelen in de andere kan totdat de ene helemaal leeg is of de andere helemaal vol. Je vindt ook een Python programma om het probleem op te lossen
Auteur archieven: admin
Vrijdag de dertiende
Toon aan dat er in ieder jaar minstens 1 en hoogstens 3 keer vrijdag de dertiende voorkomt.
- De dertiende van elke maand in een niet-schrikkeljaar hebben als dagnummer:13,44,72,103,133,164,194,225,256,286,317,347.
- De resten bij deling door 7 zijn: 6,2,2,5,0,3,5,1,4,6,2,4
- Twee maanden A en B worden in hetzelfde vakje geplaatst als de dertiende van die maanden op dezelfde dag van de week vallen. Omdat elk getal, van 0 tot 6, voorkomt in de laatste rij, zijn de maanden over de 7 vakjes verdeeld.
- Elk van de 7 vakjes stelt één van de dagen van de week voor. Omdat elk vakje bezet is, komt er minstens 1 vrijdag de dertiende voor in een niet-schrikkeljaar.
- Een zelfde waarde in dat rijtje resten komt hoogstens 3 maal voor, dus kunnen er hoogstens 3 vrijdagen de dertiende voorkomen.
- Voor een schrikkeljaar zijn de dagnummers van de dertiende: 13,44,73,104,134,165,195,226,257,287,318 en 348.
- De resten bij deling door 7 zijn: 6,2,3,6,1,4,6,2,5,0,3 en 5. De redenering is analoog als hierboven
6 januari 2023 is een vrijdag, dus zijn er in 2023 twee vrijdagen de dertiende, namelijk in januari en oktober: de dagnummers moeten modulo 7 gelijk zijn aan 6 en er komt in het rijtje dagnummers bij niet-schrikkeljaren inderdaad 2 keer een 6 voor.
Patronen
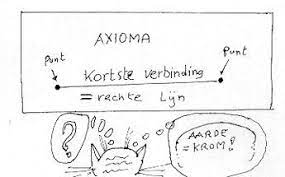
Axioma’s
Axioma’s worden op een intuïtieve manier aangebracht als een soort van spelregels. Zonder besef van een deductief systeem heeft bewijsvoering immers geen zin.
We kunnen ook de keuze van een axiomasysteem proberen toe te lichten. We mogen zo een axiomasysteem niet koesteren als een goddelijke waarheid. Anderzijds moeten we ook beseffen dat we geen totale vrijheid hebben in het combineren van axioma’s. Het systeem moet consistent zijn, dus geen tegenspraak bevatten. dat is echter moeilijk na te gaan omdat axioma’s uitspraken zijn over primitieve begrippen. Om de consistentie aan te tonen gaat men gebruik maken van een model: een concrete interpretatie van de ongedefinieerde concepten. We geven een klein voorbeeld:
- Ax1: Elke x bevat minstens één y.
- Ax2: Er zijn minstens 2 y’s.
- Ax3: Als p en q twee y’s zijn, dan is er juist 1 x die zowel p als q bevat.
- Ax4: Als a een x is, dan is er een y niet in a.
Een mogelijk model is dan : x = rechte en y = punt
Van een axiomasysteem verlangen we nog een andere eigenschap: de onafhankelijkheid. Dit wil zeggen dat geen van de axioma’s kan worden afgeleid uit de andere. Om dat na te gaan moeten we dus modellen construeren die aan alle axioma’s, behalve die ene, voldoen.
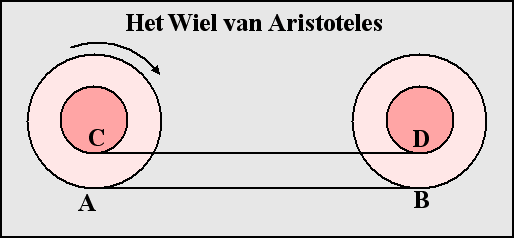
De wielparadox
Stelt u zich een klein wiel op een groot wiel voor, voorgesteld als twee concentrische cirkels. Voor elk punt op de kleine cirkel is er exact één punt op de grote cirkel en omgekeerd.Je kan dus verwachten dat het samengestelde wiel dezelfde afstand aflegt als het kleine wiel over een staaf rolt of als het grote wiel over de weg rolt. Maar dat kan toch niet, want de omtrek van beide cirkels is verschillend!
Deze paradox werd door Aristoteles beschreven in een oude Griekse tekst Mechanica.
Cantor heeft veel later aangetoond dat een een-op-eenovereenkomst van punten, niet betekent dat twee krommen even lang moeten zijn.
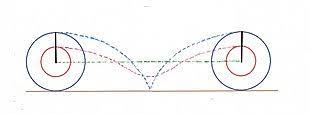
De totale verplaatsing van punten op de omtrek van een Aristoteles-wiel kan je zien op onderstaande afbeelding: