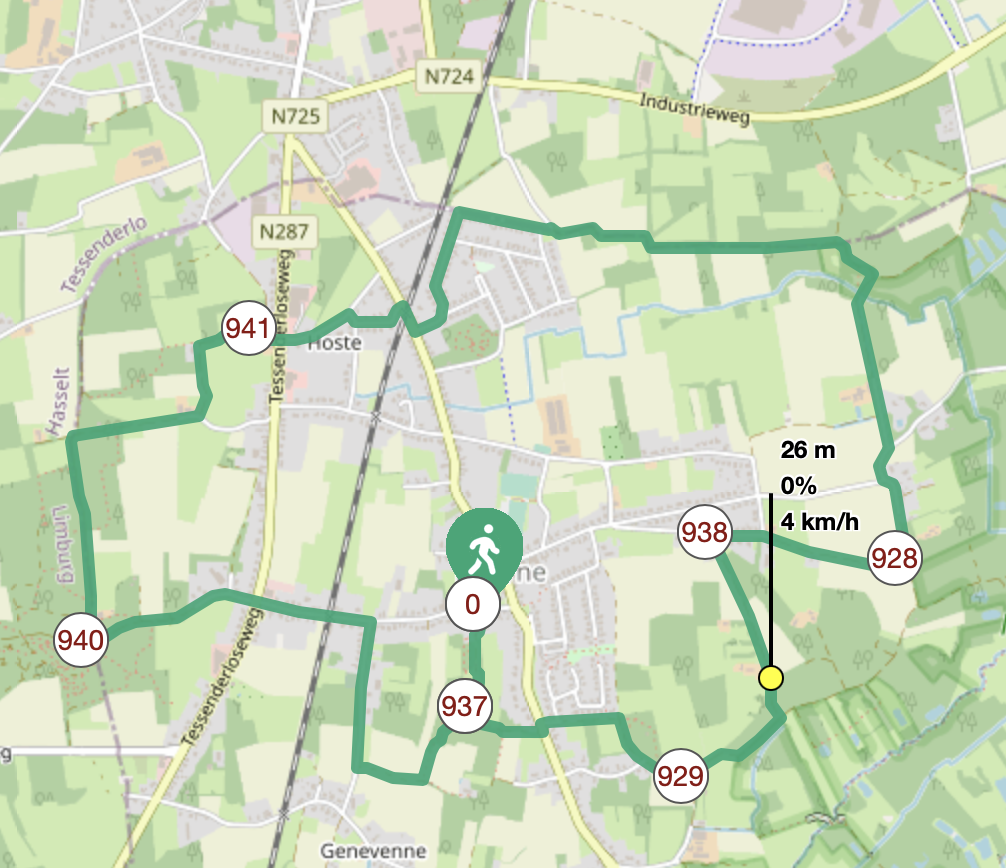
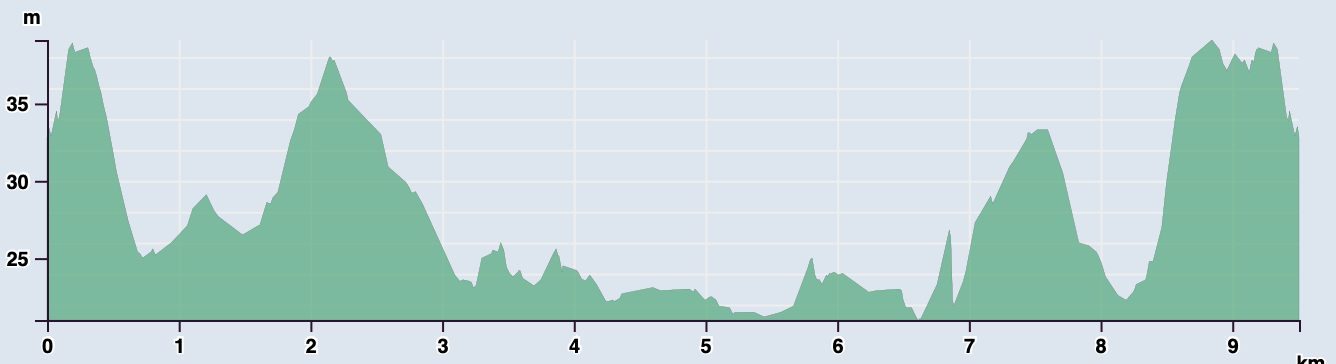
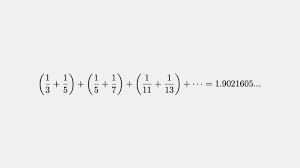Deze wandeling is ongeveer 9,5 km lang en start aan de Sint-Engelbertuskerk in Deurne, deelgemeente van Diest/
Auteur archieven: admin
De constante van Brun
Vrij veel priemgetallen zijn twee opeenvolgende oneven getallen, zoals 3 en 5 of 17 en 19. Of er oneindig veel zulke paren, priemtweelingen genoemd, zijn is niet bewezen .
In 1919 bewees de Noorse wiskundige Viggo Brun( 1885-1978) volgende eigenschap:de som van de omgekeerde waarden van de priemtweelingen nadert tot een bepaalde waarde, die nu de constante van Brun wordt benoemd.
- Het is merkwaardig dat deze som begrensd is terwijl de som van de omgekeerden van alle priemgetallen oneindig groot is. Dit laat vermoeden dat het priemtweelingen eerder schaars zijn.
- Het is onbekend of de constante van Brun een irrationaal getal is. Dit hangt ervan af of het aantal priemtweelingen eindig of oneindig is.
-
Een schatting van Pascal Sebah en Patrick Dechimel in 2002 die alle priemtweelingen tot 1016 gebruikt komt op B ≈ 1,902160583104.
Fietstocht
Chebychev metriek
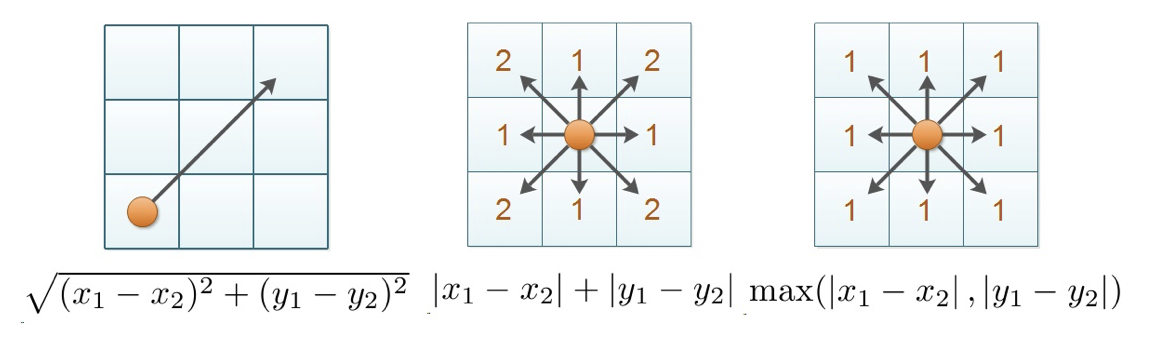
We weten allemaal hoe we de afstand meten tussen twee punten. Hierbij verzwijgen we eigenlijk dat het gaat over de euclidische afstand. Er zijn ook andere manieren om een afstand te berekenen.
Zo heb je bijvoorbeeld de Chebychev afstand ( naar de Russische wiskundige Pafnoeti Chebychev(1821-1894)) en de taximetrische afstand. Neem twee punten ![]() en
en ![]() , dan is de Chebychev afstand het maximum van de getallen
, dan is de Chebychev afstand het maximum van de getallen ![]() en de taximetrische afstand is de som van al die getallen.
en de taximetrische afstand is de som van al die getallen.
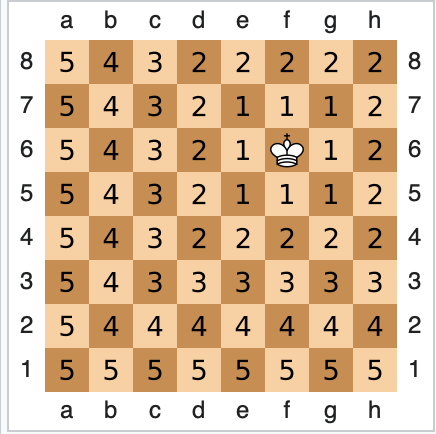
Zo is de Chebychev afstand tussen twee velden op een schaakbord het minimum aantal zetten dat de koning nodig heeft om zich van het ene punt naar het andere punt te begeven.
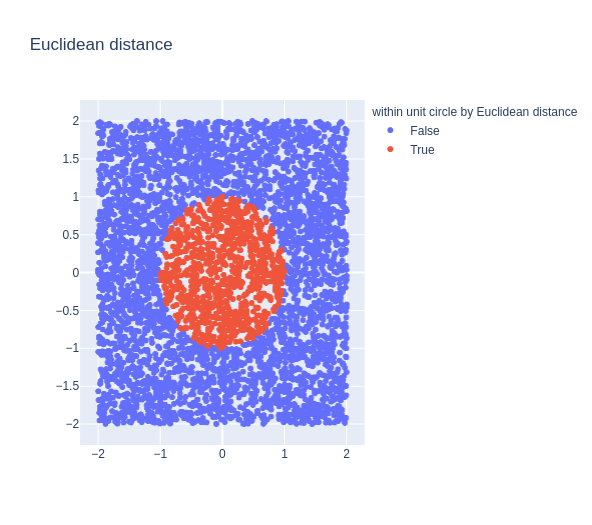
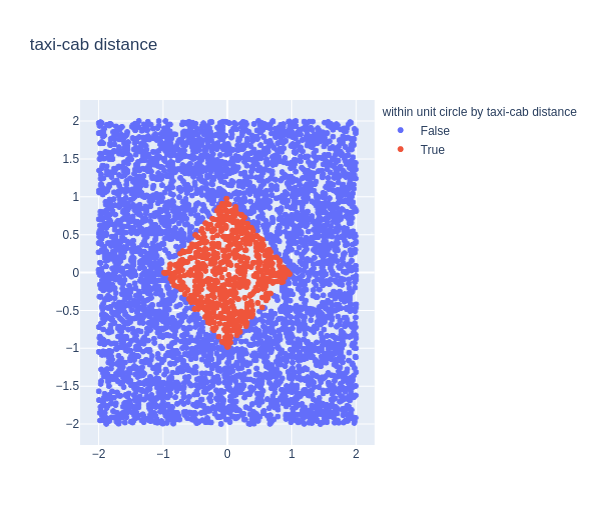
We geven tot slot nog een afbeelding van de eenheidscirkel in de drie afstanden: Euclidisch, Chebychev en taximetrisch:
Product van de delers van een getal
Noteer met i het aantal delers van een gegeven natuurlijk getal n, dat verschilt van 0. Kan je dan een formule vinden voor het product van al de delers van n?
Stel del(n) = ![]() en noteer met P(n) het product van alle delers . Dan is P(n) =
en noteer met P(n) het product van alle delers . Dan is P(n) = ![]() . Vermenigvuldigen we deze twee uitdrukkingen met elkaar :
. Vermenigvuldigen we deze twee uitdrukkingen met elkaar : ![]() , dan vinden we
, dan vinden we
![]()
Enkele voorbeelden:
- del(7) = (1,7} , dus
 en 1*7=7
en 1*7=7 - del(9) = (1,3,9} , dus
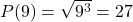 en 1*3*9=27.
en 1*3*9=27. - del(12) = (1,2,3,4,6,12} , dus
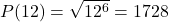 en 1*2*3*4*6*12=1728.
en 1*2*3*4*6*12=1728.