Auteur archieven: admin
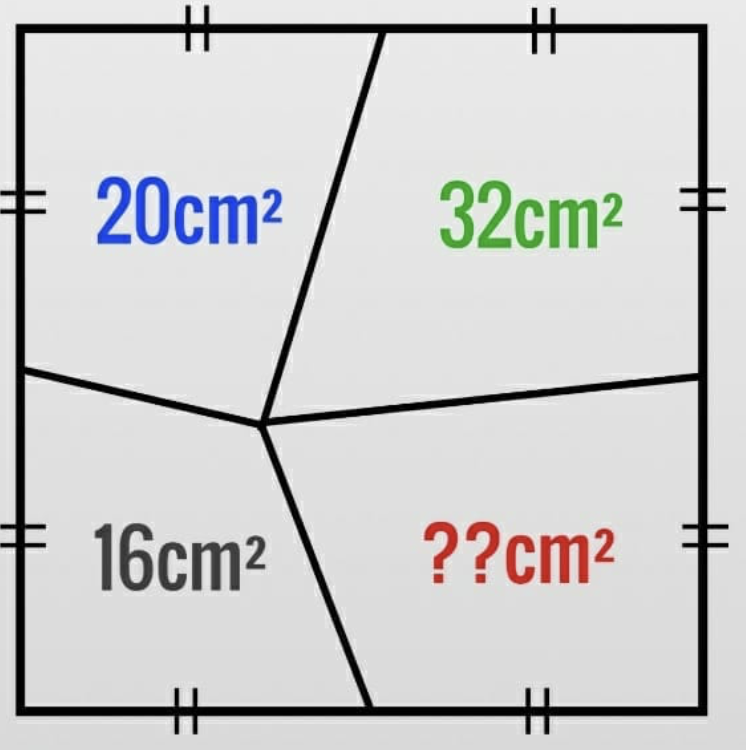
Nootje 38
- Onderverdelen in driehoeken lijkt een goed idee:
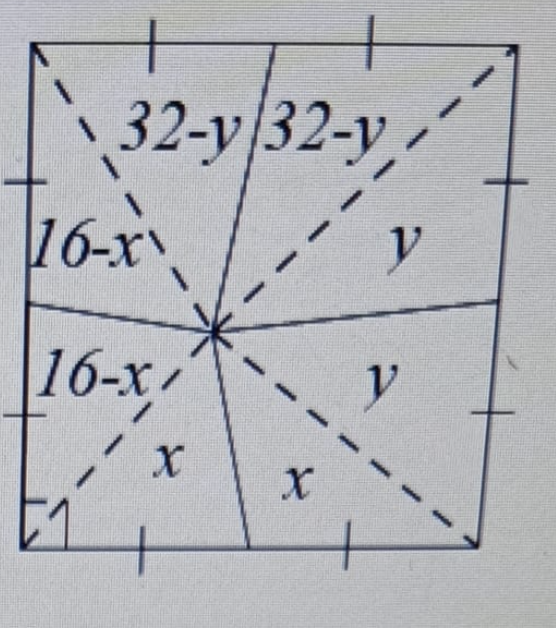
- De gelijkheid van oppervlaktes is evident: zelfde hoogte en even grote basis.
- De vierhoek linksboven heeft oppervlakte 20 en is dus gelijk aan
 .
. - Hieruit volgt
 .
. - De oppervlakte van de vierhoek rechts onder, die gevraagd wordt, is gelijk aan
 , dus de gevraagde oppervlakte is gelijk aan 28 vierkante centimeter.
, dus de gevraagde oppervlakte is gelijk aan 28 vierkante centimeter.
Nootje 37
Een gouden driehoek
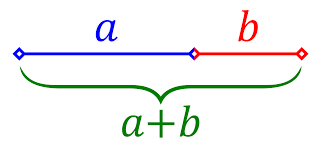
Bij de gulden snede verhoudt het grootste van de twee delen zich tot het kleinste, zoals het gehele lijnstuk zich verhoudt tot het grootste. Geven we het grootste deel aan met a en het kleinste deel met b, dan is de verhouding van beide zo dat ![]() . De bedoelde verhouding
. De bedoelde verhouding ![]() noemt men het gulden getal en noteert men met
noemt men het gulden getal en noteert men met ![]() . Het oplossen van de gegeven vergelijking geeft:
. Het oplossen van de gegeven vergelijking geeft:
![]()
Waar kunnen we in een driehoek dit gulden getal zien?
Neem een gelijkbenige driehoek met basishoeken van ![]() :
: 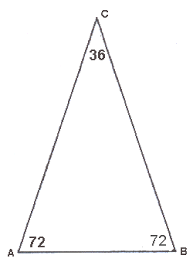
De hoogtelijn uit C verdeelt de overstaande zijde in twee gelijke stukken en de tophoek in twee gelijke hoeken. Zo een halve tophoek meet dan ![]() . Dan is
. Dan is ![]() en
en ![]() . Bijgevolg is
. Bijgevolg is ![]() . Gebruiken we nu formules voor de dubbele en drievoudige hoek:
. Gebruiken we nu formules voor de dubbele en drievoudige hoek: ![]() .
.
Vermits ![]() , kunnen we beide leden delen door
, kunnen we beide leden delen door ![]() en als we dan de grondformule van de goniometrie toepassen, vinden we
en als we dan de grondformule van de goniometrie toepassen, vinden we
![]()
In de bovenstaande driehoek is ![]() , dus
, dus
![]()
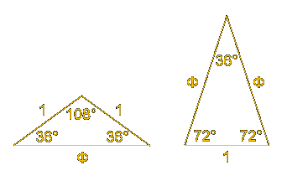
Zoals je in bovenstaande tekening ziet, kan je dit ook verkrijgen met een gelijkbenige driehoek met basishoeken van ![]() .
.
Nootje 36
Vind alle niet complexe oplossingen van
![]()
- Alles uitrekenen geeft een vierdegraadsvergelijking, die waarschijnlijk niet op te lossen is.
- We gaan de factoren in het linkerlid twee per twee uitrekenen: de eerst met de laatste en de twee middelsten.
- De opgave wordt dan:
 .
. - We merken op dat de twee eerste termen van de tweede factor het viervoud zijn van de eerste twee termen van de eerste factor. Stel

- We krijgen dan
 of na uitwerken
of na uitwerken  .
. - Deze vierkantsvergelijking heeft als oplossingen 1 en
 .
. - Vervangen we y terug dan verkrijgen we twee vergelijkingen van de tweede graad. De eerste
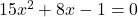 geeft als oplossingen
geeft als oplossingen  .
. - De tweede vergelijking wordt
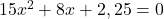 en deze heeft geen reële oplossingen.
en deze heeft geen reële oplossingen. - De enige niet complexe oplossingen zijn dus
![Rendered by QuickLaTeX.com \[\frac{-4\pm \sqrt{31}}{15}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-d6b7fa37403b1336ecf4c59a837e61ec_l3.png?media=1678572382)