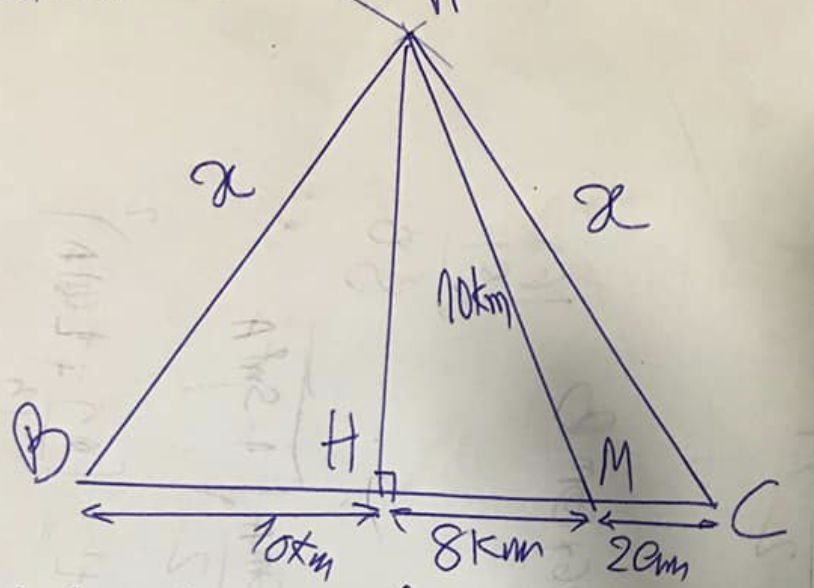
Antwoord
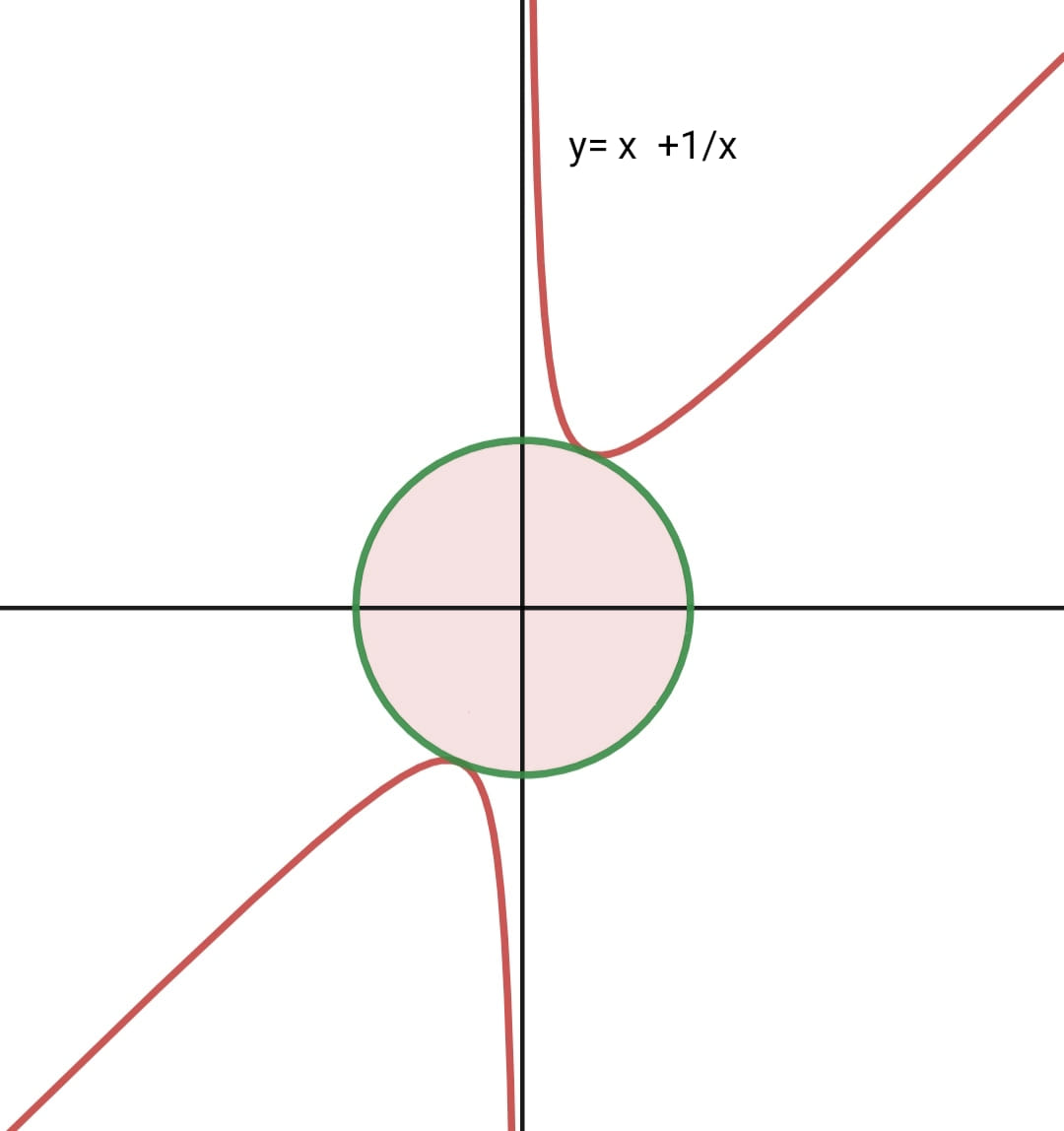
- We zoeken de vergelijking van de groene cirkel , met middelpunt de oorsprong en straal r:
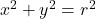 .
.  is de vergelijking van de bovenste halve cirkel
is de vergelijking van de bovenste halve cirkel- De cirkel raakt aan de rode kromme g(x) in P(x,y) als en slechts als
 en
en 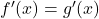 .
. - De eerste betrekking betekent dat

- De tweede betrekking geeft:
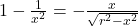
- Hieruit volgt dat
 .
. - Uitrekenen geeft
![Rendered by QuickLaTeX.com x=\frac{1}{\sqrt[4]{2}}](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-eced290af53de4114f0374bef4fefa38_l3.png?media=1678572382) . En bijgevolg is
. En bijgevolg is ![Rendered by QuickLaTeX.com y=\frac{1}{\sqrt[4]{2}}+\sqrt[4]{2}](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-810aacb74caa621731d49c1e663ffa7b_l3.png?media=1678572382) .
. - Nu is
 , dus is
, dus is  .
. - De vergelijking van de groene cirkel is:
![Rendered by QuickLaTeX.com \[x^2+y^2=2+2\sqrt{2}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-52033a4a4d1ada930e264fbb32a133bb_l3.png?media=1678572382)