Antwoord
- Stel
 ; Dan is
; Dan is  of
of  .
. - De oplossingen hiervan zijn
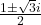 . Het is duidelijk dat de ene oplossing x voorstelt en de andere
. Het is duidelijk dat de ene oplossing x voorstelt en de andere  .
. - We kunnen deze complexe oplossingen ook schrijven met behulp van de goniometrische notatie:
 en
en  .
. - Nu moeten we
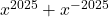 uitrekenen. We doen dit met de formule van Le Moivre.
uitrekenen. We doen dit met de formule van Le Moivre.  . Een oneven veelvoud van
. Een oneven veelvoud van  maakt de cosinus -1 en de sinus 0.
maakt de cosinus -1 en de sinus 0.- Dus
 . Analoog kunnen we
. Analoog kunnen we  uitrekenen en we vinden
uitrekenen en we vinden  .
. - Bijgevolg is de gevraagde uitdrukking gelijk aan -2.








