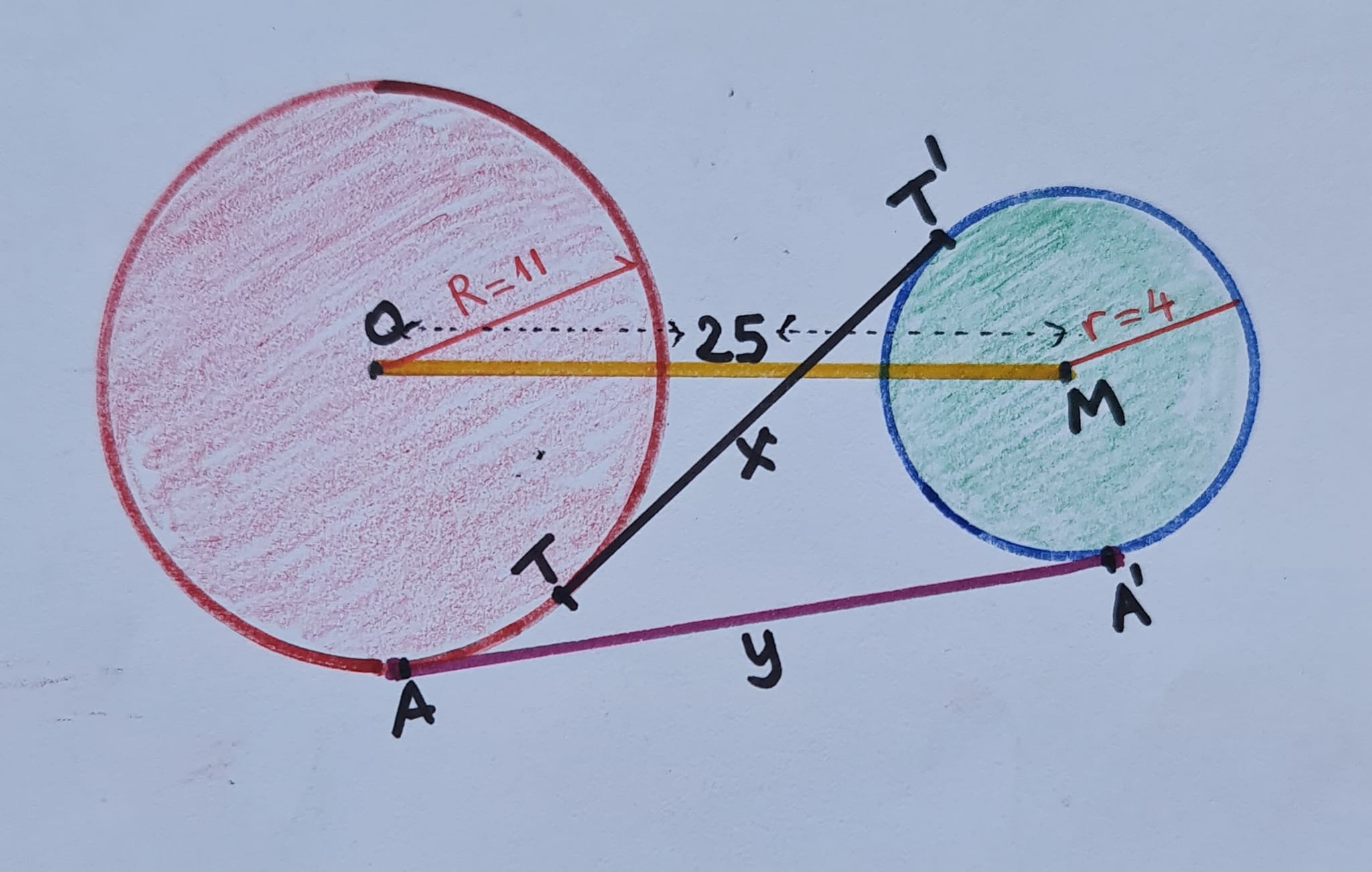
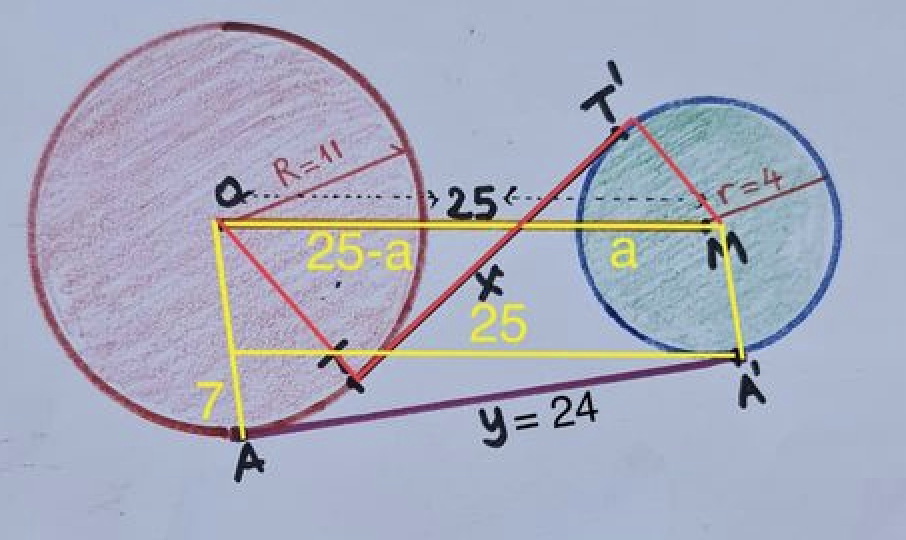
Gegeven zijn twee cirkels met stralen 4 en 11. De afstand tussen hun middelpunten is 25. Bepaal de som van de lengtes van een inwendig en een uitwendig gemeenschappelijke raaklijn.
Auteur archieven: admin
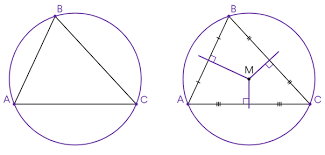
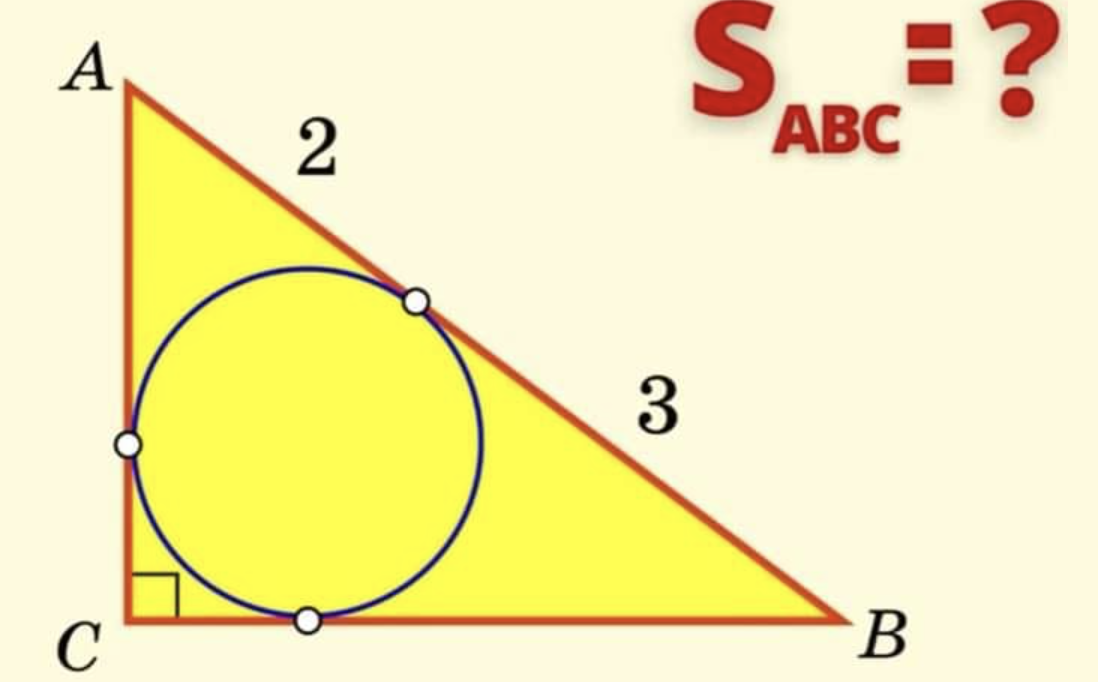
Straal in en omgeschreven cirkel
De Kepler-Bouwman constante
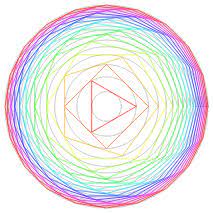
Teken een cirkel met straal 1. Teken een regelmatige ( dus gelijkzijdige) driehoek, omgeschreven aan deze cirkel. Teken vervolgens de omgeschreven cirkel van die driehoek en het vierkant omgeschreven aan die cirkel. Daarna teken je weer de omgeschreven cirkel van dat vierkant en een regelmatige vijfhoek omgeschreven aan die cirkel. Ga daar oneindig mee door.
We zouden kunnen verwachten dat je zo steeds grotere cirkel gaat bekomen. En hoewel de cirkels aanvankelijk groter worden, neemt de mate van groter worden steeds af en zullen de stralen van de omgeschreven cirkels naderen tot een bepaalde limietwaarde.
Die waarde lijkt niet zo moeilijk om uit te rekenen. 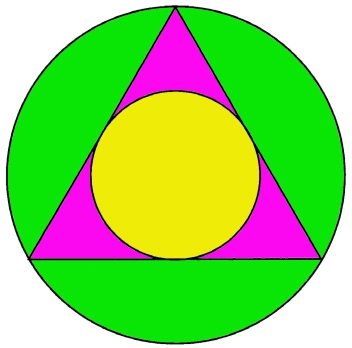
De verhouding van de stralen van de gele en groene cirkel is ![]() . Hieruit volgt dat de gezochte limietwaarde het omkeerde is van
. Hieruit volgt dat de gezochte limietwaarde het omkeerde is van
![Rendered by QuickLaTeX.com \[\prod_{k=3}^{\infty}\cos \frac{\pi}{k}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-8391198401adcea5e820f670ab6da3ca_l3.png?media=1678572382)
De eerste die dit deden waren Edward Kasner (1878-1955) en James Newman (1907-1966). Zij bekwamen een waarde van ongeveer 12. In 1965 gaf een Nederlandse wiskundige Christoffel Bouwkamp (1915-2003) als waarde 8,7000 aan.`
Nootje 40
Als  , bereken dan
, bereken dan
![]()