Omdat ggd(a,b,c) = ggd( ggd(a,b),c) kunnen we recursief werken. Neem als voorbeeld de vergelijking
![]()
- Herschrijf deze vergelijking als
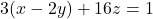 .
. - Stel
 , dan wordt de gegeven vergelijking
, dan wordt de gegeven vergelijking  .
. - Gebruikmakend van de techniek uit les 1 vinden we dat
 en
en  , met t een willekeurig geheel getal.
, met t een willekeurig geheel getal. - Met dezelfde methode kunnen we via
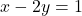 , de oplossing van
, de oplossing van  schrijven als
schrijven als  en
en 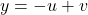 met v een geheel getal.
met v een geheel getal. - Na eliminatie van u vinden we dus dat
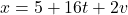 ,
,  en
en  . Dit zijn alle gehele oplossingen van de gegeven vergelijking. Deze hangen af van 2 parameters.
. Dit zijn alle gehele oplossingen van de gegeven vergelijking. Deze hangen af van 2 parameters.