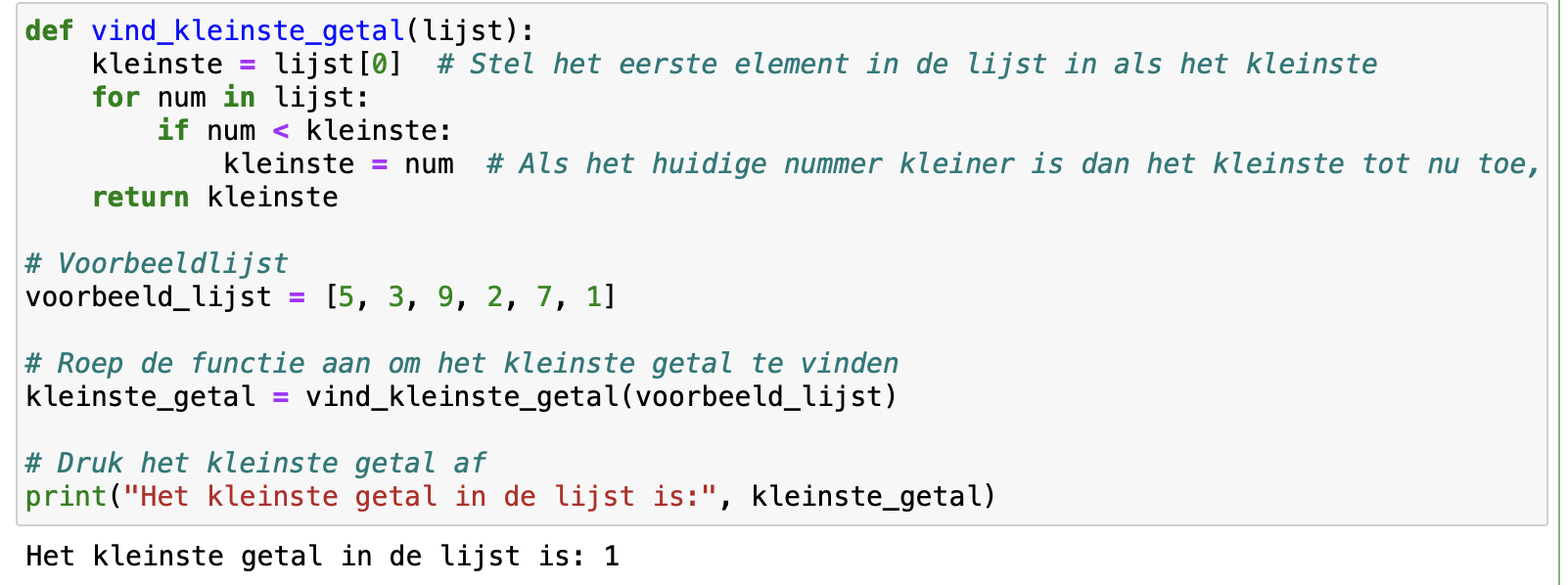
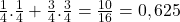Een Python programma om het kleinste getal in een lijst terug te vinden:
Auteur archieven: admin
Nootje 46
Bereken
![]()
Antwoord
Dames in een kaartspel
Schud een spel kaarten goed. Hoeveel kaarten van de top , gemiddeld genomen, kom je de eerste dame tegen?
- We weten dat er 4 dames in het spel zijn.
- Wat ook de volgorde van de kaarten mag zijn, de dames verdelen het pak kaarten in 5 groepen: de kaarten voor de eerste dame, de kaarten tussen de eerste en tweede dame, enzovoort.
- Het aantal kaarten in elk van die groepen varieert van 0 tot en met 48.
- Noteer met
 het aantal kaarten in de i-de groep. Dan geldt:
het aantal kaarten in de i-de groep. Dan geldt: ![Rendered by QuickLaTeX.com \[0 \leq X_i \leq 48\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-ba2b507c09a658d2fe2ffcc7084a6ae9_l3.png?media=1678572382)
![Rendered by QuickLaTeX.com \[X_1+X_2+X_3+X_4+X_5=48\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-65cda2951fedf127f5d52d5aa6910813_l3.png?media=1678572382)
- Elke
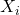 is een kansvariabele en omdat het pak kaarten goed geschud is, zal de kansverdeling van elke
is een kansvariabele en omdat het pak kaarten goed geschud is, zal de kansverdeling van elke 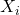 dezelfde zijn.
dezelfde zijn. - Maar dan is
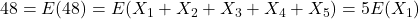 .
. - Bijgevolg is
![Rendered by QuickLaTeX.com \[E(X_1)=\frac{48}{5}=9,6\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-50f79ad0e630b542d93d616e003405ab_l3.png?media=1678572382)
- Het verwacht aantal kaarten voor de eerste dame is dus gelijk aan
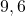 .
.
Determinant vervolg
Bereken de kans dat de determinant van een 3×3 matrix, met natuurlijke getallen als elementen, oneven is.
- Gegeven een matrix
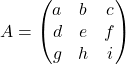 .
. - Zijn determinant is
![Rendered by QuickLaTeX.com \[det A =aei+bfg+dhc-gec-dbi-ahf\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-488f7b5bb7a20f5ecd7df36f05508736_l3.png?media=1678572382)
- Omdat het gaat over even/oneven kunnen we modulo 2 werken.
- Determinant oneven betekent dan dat de determinant 1 is en dus dat de matrix inverteerbaar moet zijn.
- Een matrix is inverteerbaar als de kolommen onafhankelijk zijn. Kies de eerste kolom willekeurig ( mag niet 000 zijn) . Dan heb je hiervoor 7 mogelijkheden.
- De tweede kolom mag geen veelvoud zijn van de eerste, maw mag er niet aan gelijk zijn. Dus heb je hiervoor nog 6 mogelijkheden.
- De derde kolom mag niet gelijk zijn aan de eerset of de tweede , maar ook niet gelijk aan de som van die twee ( en natuurlijk ook niet 000). Hiervoor heb je 4 mogelijkheden .
- Er zijn 7x6x4=168 mogelijkheden om determinant 1 te vinden. Er zijn
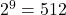 mogelijke matrices te vormen met nullen en enen.
mogelijke matrices te vormen met nullen en enen. - De kans dat een 3×3 matrix met natuurlijke elementen oneven is , is dus
![Rendered by QuickLaTeX.com \[\frac{168}{512}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-d18444542bf1fa1c77aee68a871e8245_l3.png?media=1678572382)
Determinant
Bereken de kans dat de determinant van een 2×2 matrix, met natuurlijke getallen als elementen, even is.
- Gegeven een matrix
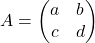 .
. - Zijn determinant is
![Rendered by QuickLaTeX.com \[det A =ad-bc\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-9fede75da8aa1d4494d87db6c92374bf_l3.png?media=1678572382)
- Een product van twee natuurlijke getallen is oneven als beide getallen oneven zijn, dus de kans dat
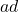 oneven is, is
oneven is, is  . De kans dat
. De kans dat 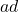 even is, wordt dat
even is, wordt dat 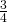 .
. - Nu is
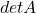 even als
even als 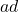 en
en 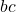 beiden even zijn of beide oneven zijn.
beiden even zijn of beide oneven zijn. - De kans dat
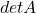 even is , is bijgevolg gelijk aan
even is , is bijgevolg gelijk aan