Algebraïsche getallen | Wiskunde is leuk

Een algebraïsch getal is een wortel van een van 0 verschillende veelterm met rationale coëfficiënten.

Zo is $\sqrt{2}$ een reëel algebraïsch getal want $\sqrt{2}$ is een wortel van de veelterm $x^2-2$ . Verder is bijvoorbeeld $\sqrt{2}i$ een complex algebraïsch getal want $\sqrt{2}i$ is een wortel van de veelterm $x^2+2$ .

Enkele eigenschappen:

het tegengestelde van een algebraïsch getal is ook een algebraïsch getal.
het omgekeerde van een van 0 verschillend algebraïsch getal is ook een algebraïsch getal.
elk rationaal getal is een algebraïsch getal.
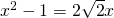ook de som en het product van 2 algebraïsche getallen zijn algebraïsch. Dit is niet zo evident. Neem bijvoorbeeld $x=\sqrt{2}+\sqrt{3}$ , de som van 2 algebraïsche getallen. Dan is $x-\sqrt{2}=\sqrt{3}$ , wat na kwadrateren $x^2-1=2\sqrt{2}x$ geeft. Nogmaals kwadrateren geeft uiteindelijk 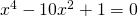$x^4-10x^2+1=0$ .Bijgevolg is $x$ een algebraïsch getal.
uit al de vorige eigenschappen kan je dus besluiten dat de algebraïsche reële getallen en de algebraïsch complexe getallen, allebei met de gewone optelling en vermenigvuldiging, velden zijn.
men kan zelfs bewijzen dat r een reëel algebraïsch getal is als r een wortel is van een van 0 verschillende veelterm met gehele coëfficiënten.
we noteren $\mathbb{A}$ voor het veld van de reële algebraïsche getallen. Dan is $\mathbb{Q} \subset \mathbb{A}\subset \mathbb{R}$ .

Een transcendent getal is een getal dat niet algebraïsch is. Het bestaan van transcendente getallen is niet vanzelfsprekend. dat ze inderdaad bestaan is bewezen door de Franse wiskundige J.Liouville(1809-1882).

De transcendentie van e, de basis van de natuurlijke logaritmen, werd in 1873 bewezen door C.Hermite(1829-1901). De transcendentie van $\pi$ werd op een gelijkaardige manier bewezen in 1882 door F.Lindemann(1852-1939)

Cantor bewees dat de verzameling van de complexe algebraïsche getallen aftelbaar oneindig is, met andere woorden ze bezit dezelfde kardinaliteit als de verzameling van de natuurlijke getallen. De stelling van Cantor houdt in dat de verzameling van de transcendente complexe getallen de overaftelbaar is. Dus bijna alle complexe getallen zijn transcendent! In de beginafbeelding zie je de algebraïsche complexe getallen.