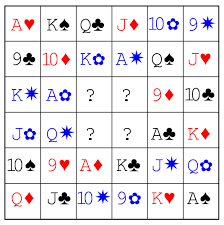
Het 36 officieren probleem, ook wel bekend als het probleem van Euler’s 36 officieren, is een beroemde puzzel in de combinatoriek, bedacht door de wiskundige Leonhard Euler in 1782. Het probleem kan als volgt worden omschreven:

Stel je hebt een leger van 36 officieren, bestaande uit 6 verschillende regimenten en 6 verschillende rangen. Je moet deze 36 officieren opstellen in een 6×6 rooster, zodanig dat in elke rij en elke kolom precies één officier van elk regiment en één officier van elke rang voorkomt.

Euler conjectureerde dat dit probleem geen oplossing heeft voor een 6×6 rooster, en dit werd later bewezen door Gaston Tarry (1843-1913) in 1901. Het betekent dat het onmogelijk is om een 6×6 rooster te vullen met deze eigenschappen. De onmogelijkheid van het oplossen van het 36-officieren probleem komt voort uit het feit dat het een speciaal geval is van het algemene probleem van het vinden van “orthogonale Latijnse vierkanten”. Latijnse vierkanten zijn roosters waarbij in elke rij en kolom elke symbool precies één keer voorkomt. Twee Latijnse vierkanten zijn orthogonaal als je ze over elkaar legt en elke combinatie van symbolen precies één keer voorkomt. Voor n=6 bestaat er geen paar van orthogonale Latijnse vierkanten, wat het 36-officieren probleem onoplosbaar maakt.

Euler vermoedde dat als , waarbij k een natuurlijk getal is, er geen paar orthogonale Latijnse vierkanten van bestaat. Dit vermoeden werd pas in 1959 ontkracht, toen de wiskundigen Bose,Shikhande en Parker een paar orthogonale Latijnse vierkanten van maakten. 

Er bestaan wel oplossingen als bijvoorbeeld   en