Aan de hand van enkele voorbeelden bespreken we Diophantische vergelijkingen: dit zijn vergelijkingen met gehele coëfficiënten waarvan gehele oplossingen gevraagd worden.
We starten in les 1 met de basisvergelijking ![]() met
met ![]() . Neem bijvoorbeeld
. Neem bijvoorbeeld ![]() .
.
- Omdat de grootste gemene deler van 7 en 13 gelijk is aan 1 en dit een deler is van 81, heeft deze vergelijking oplossingen.
- Volgens de stelling van Bezout kunnen we deze grootste gemene deler schrijven als een lineaire combinatie van 7 en 13. Dat kan door het recursief gebruiken van het algoritme van Euclides voor het bepalen van de grootste gemene deler.
- Zo is
 en dus is
en dus is 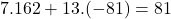 . Bijgevolg is
. Bijgevolg is 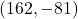 een particuliere oplossing van de gegeven vergelijking.
een particuliere oplossing van de gegeven vergelijking. - Als we nu de twee vergelijkingen
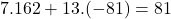 en
en 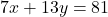 van elkaar aftrekken vinden we
van elkaar aftrekken vinden we  . Bijgevolg is 7 een deler van
. Bijgevolg is 7 een deler van 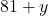 en 13 een deler van
en 13 een deler van  .
. - Er bestaat dus een geheel getal t zodat
en dus is![Rendered by QuickLaTeX.com \[\frac{162-x}{13}=\frac{81+t}{7}=t\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-62386967d1eab26a466f398b5ee613c8_l3.png?media=1678572382)
 en
en 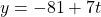 . Alle gehele oplossingen van de gegeven vergelijking zijn van deze vorm.
. Alle gehele oplossingen van de gegeven vergelijking zijn van deze vorm.
