In de wiskunde zijn er verschillende  stellingen die elk op hun eigen manier zeggen dat totale wanorde onmogelijk is.  Zo hebben we bijvoorbeeld het vermoeden van Baudet: Als je de hele verzameling in twee verzamelingen A en B verdeelt, is het dan noodzakelijk zo dat (ten minste) één van die twee verzamelingen willekeurig lange rekenkundige rijtjes bevat?

De Nederlandse wiskundige Van der Waerden publiceerde in 1927 een bewijs. In het artikel staat een algemenere bewering :  voor elk paar positieve gehele getallen r en k is er een getal N zodanig dat indien men {1, 2, …, N }  in r  klassen verdeelt, er minstens een klasse is die een rekenkundige rij van lengte k bevat. Het kleinste getal N waarvoor dit geldt noemt men het Van der Waerden-getal W(r,k).

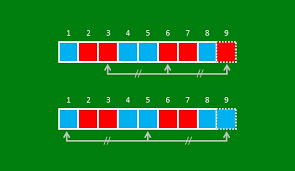
Zo is bijvoorbeeld W(2,3) =  9. Een kleinere waarde is er niet want {{1,2,4,5},{3,4,6,8}} is een verdeling van {1,2,3,4,5,6,7,8} in twee delen die geen rekenkundige rij met 3 elementen bevat. In onderstaande tekening kleur je de getallen van 1 tot en met 9 in 2 kleuren; je ziet dat je steeds een rekenkundige rij van drie elementen krijgt in eenzelfde kleur.