Gegeven is 
. Bepaal de minimumwaarde van 
.
Antwoord
- Je zou natuurlijk gebruik kunnen maken van de parametervergelijking van de cirkel en zeggen dat
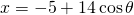en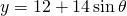 
. Dit invullen in geeft een functie in één variabele : 
. Via de theorie van afgeleiden kan je dan de minimale waarde vinden. - Maar als je de vraag meetkundig bekijkt kom je sneller tot een oplossing. We zoeken eigenlijk naar een punt op de gegeven cirkel dat het dichtst bij de oorsprong ligt. maar dat ligt dit punt A op dezelfde lijn als het middelpunt van de cirkel (M) en de oorsprong. Omdat de afstand van A tot M 14 is en de afstand van M tot O 13 is, zal de minimale waarde van gelijk zijn aan 1.