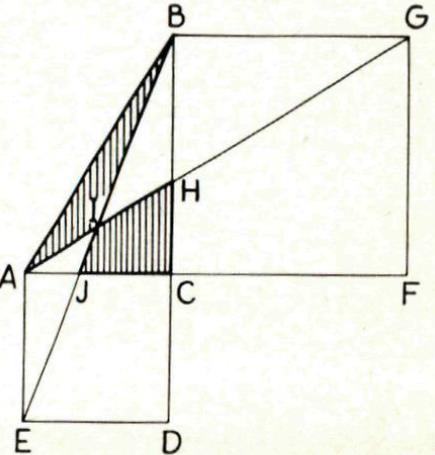
Op de zijden van een rechthoekige driehoek ABC tekent men twee vierkanten: BGFC en AEDC. De rechten AG en BE snijden elkaar in I. Verder is H het snijpunt van AG met BC en J het snijpunt van BE met AC. Bewijs dat de oppervlakte van ABI gelijk is aan de oppervlakte van IHJC.