Bereken de vierkantswortel van x met
![]()
Antwoord
Antwoord
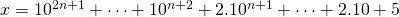 .
.- De termen met een factor 2 splitsen we op en we schrijven 5 als 1+1+3.
- We vinden dan
 .
. - Gebruiken we nu de partiële som formule voor de termen van een meetkundige rij:
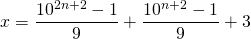
- We brengen op gelijke noemer:
 .
. - Dan is
 .
. - Hieruit volgt dat
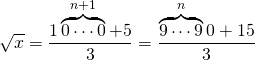 .
. - Uiteindelijk vinden we dat de vierkantswortel van x gelijk is aan
![Rendered by QuickLaTeX.com \[\overbrace{3\cdots3}^n5\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-c55d3d97af5143f501a36b076ab8b339_l3.png?media=1678572382)
