Sommige stellingen zijn zo eenvoudig en elegant dat je jezelf kan afvragen: Waarom ben ik daar niet zelf op gekomen?  Dit geldt onder andere  voor de volgende stelling die vernoemd wordt naar zijn ontdekker: de Oostenrijkse wiskundige Georg Alexander Pick, geboren in 1859 in Wenen en overleden in 1942 in het concentratiekamp  Theresienstadt.

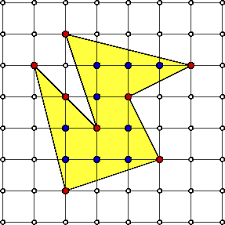
Het gaat over de oppervlakte van een roosterveelhoek, dit wil zeggen een veelhoek waarvan de hoekpunten op de punten van een regelmatig vierkant rooster liggen. Noteer met het aantal roosterpunten op de rand van de veelhoek V en met het aantal roosterpunten in het inwendige van V.

Voor deze veelhoek is de oppervlakte dus oppervlakte eenheden.