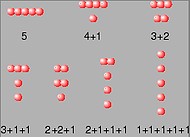
Al eeuwenlang proberen de knapste wiskundekoppen grip te krijgen op de zogeheten partitiefunctie. Deze functie geeft aan op hoeveel manieren een aantal knikkers kan worden opgedeeld in groepjes. Zo kun je 5 knikkers bijvoorbeeld verdelen in vier groepjes: één groepje van 2 en drie groepjes van 1. Als som kun je dit schrijven als 5 = 2 + 1 + 1 + 1. Een andere partitie is 5 = 3 + 2 (twee groepjes). Ook 5 = 1 + 1 + 1 + 1 + 1 (vijf groepjes) en 5 = 5 (één groepje) zijn partities. In totaal zijn er 7 partities van 5. We noteren dat als p(5) = 7.
In het algemeen geven we het aantal partities van n aan met p(n). De rij partitiegetallen is de rij p(1), p(2), p(3), p(4), p(5) enzovoorts. Die rij ziet er zo uit: 1, 2, 3, 5, 7, 11, 15, 22, ….
De getallen in die rij worden al snel ongelofelijk groot. Zo is p(20) = 627 en p(100) is al meer dan 190 miljoen.
Grote namen als Euler en Ramanujan hebben diepe inzichten verkregen in de theorie van partities. Hoewel zij met hun berekeningen veel vragen konden beantwoorden, riepen hun berekeningen uiteindelijk nog meer vragen op, waarop ook zij het antwoord schuldig moesten blijven.
Wiskundige Ken Ono heeft met een aantal collega’s nieuwe grote vorderingen gemaakt op het gebied van partities. Het team onder leiding van Ono wist te bewijzen dat de partitiegetallen zich in zekere zin gedragen als fractals, een resultaat dat niemand eerder voor mogelijk had gehouden. Zij hebben deelbaarheidseigenschappen van partities ontrafeld en een theorie ontwikkeld die de ‘oneindig herhalende’ structuur verklaart. Bovendien hebben ze de eerste eindige formule opgesteld om partitiegetallen te berekenen.
“We hebben bewezen dat partitiegetallen een ‘fractale structuur’ hebben voor elk priemgetal. Deze getallen zijn ‘zelfherhalend’ in a shocking way”, aldus Ono. “Met onze methode hebben we een antwoord gevonden op diverse vragen die tot nu toe nog open stonden.” Ongetwijfeld zullen de nieuwe resultaten leiden tot veranderingen in hoe wiskundigen partities bestuderen.