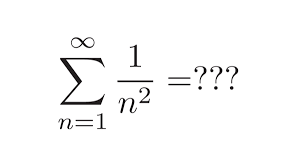Het probleem van Bazel is een beroemd probleem uit de staltheorie. Het werd voor het eerst in 1644 aan de orde gesteld door Pietro Mengoli (1626-1686), en werd bijna 100 jaar later, in 1735, opgelost door Euler.

Het probleem vraagt:

Deze reeks is bij benadering gelijk aan 1,644934.  Euler slaagde erin de exacte uitkomst te geven: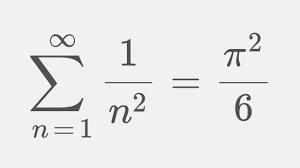

Het probleem heeft geleid tot nieuwe inzichten in de structuur van de reële getallen en de complexe getallen, en heeft bijgedragen tot de ontwikkeling van de analytische getaltheorie.

De Riemann-zeta functie is een belangrijke functie in de wiskunde vanwege het verband met de verdeling van de priemgetallen. De bovenstaande reeks is niets minder dan . Het omgekeerde getal   is de kans dat twee willekeurige gehele getallen onderling ondeelbaar zijn.