Koning Narmer

Geplaatst op 26 maart 2023 door admin

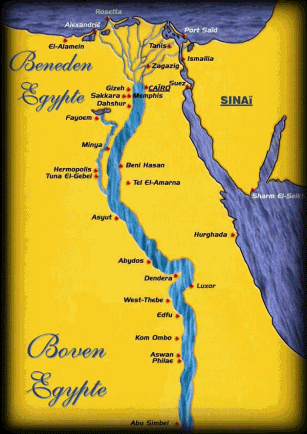
Een koning die volgens de hiërogliefen Narmer heet, maar die ook bekend staat als Menes, verenigt rond 3000 B.C. de beide Egyptische koninkrijken Boven- en Beneden-Egypte tot één staat. Met deze koning begint de eerste dynastie van het Verenigde Egyptische koninkrijk.

Om het prestige van zijn overwinning kracht bij te zetten heeft Narmer volgend palet laten maken waarop zijn overwinning op het noorden wordt uitgebeeld.

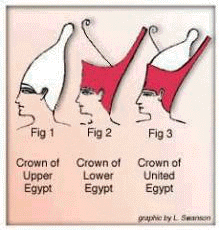
Hij draagt hierop nog de witte kroon van Boven (upper) Egypte.

De koning is de belichaming van goddelijke macht op aarde. Narmer haalt dan ook als de hemelgod Horus zijn overwinning op Beneden Egypte en in diens tempel wordt het palet opgesteld.

Nootje 32

Geplaatst op 23 maart 2023 door admin

Antwoord

Neem de veelterm V(x) met a,b en c als wortels.
Dan is $V(x)=(x-a)(x-b)(x-c)$ .
Uitgewerkt geeft dit: $V(x)=x^3-S_1x^2+S_2x-S_3$ . Hierbij is $S_1=a+b+c=1$ , $S_2=ab+bc+ac=2$ en $S_3=abc=3$ .
Bijgevolg is $V(x)=x^3-x^2+2x-3$ met $V(a)=V(b)=V(c)=0$ .
Hieruit volgt dat $a^3=a^2-2a+3$ . En dus is $a^4=a^3-2a^2+3a=-a^2+a+3$ . Er zijn gelijkaardige formules voor b en c.
Nu is $a^4+b^4+c^4=-(a^2+b^2+c^2)+(a+b+c)+9=-((a+b+c)^2-2(ab+ac+bc))+10=13$ .

Norbertijnenwandeling

Geplaatst op 19 maart 2023 door admin

Een wandeling van ongeveer 10 km rond de abdij van Averbode met verrassend toch wat hoogtemeters. Gebruik de wandelknooppunten van de Merode:

Som gelijk aan product

Geplaatst op 17 maart 2023 door admin

Noteer alle niet-triviale n-de machtswortels uit 1 door $e_i:i=2....n$ . Stel $e_1=1$ . Vorm nu de uitdrukkingen $a_i=1-e_i$ en bewijs dat

$\sum_{i=2}^na_i=\prod_{i=2}^na_i$

$z^n-1=(z-1)(z-e_2)(z-e_3)...(z-z_n)=(z-1)(z^{n-1}+...+z+1)$
Dus is $(z-e_2)(z-e_3)...(z-z_n)=z^{n-1}+...+z+1$
Stel hierin $z=1$ en je vindt dat het rechterlid uit de te bewijzen formule gelijk is aan $n$ .
Verder is het linkerlid gegeven door $\sum_{i=2}^na_i=\sum_{i=1}^na_i= \sum_{i=1}^n1-\sum_{i=1}^ne_i=n-0=n$ .
Bij de laatste stap maken we gebruik van de eigenschap dat de som van de wortels van $z^n-1$ gelijk is aan de coëfficiënt van de op één na hoogste graadsterm.
Hiermee is het gestelde bewezen.