Sangaku 11

Geplaatst op 29 december 2022 door admin

Antwoord

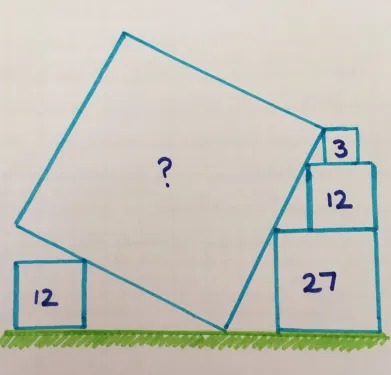
De bedoeling is de oppervlakte van het vierkant te bepalen.
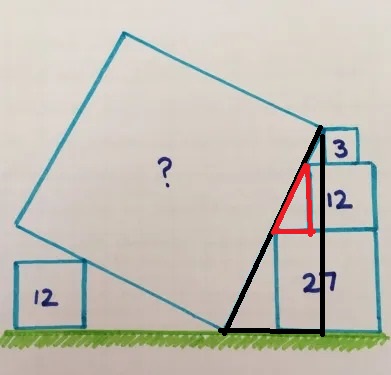
De horizontale rechthoekzijde van de rode driehoek is gelijk aan 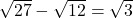$\sqrt{27}-\sqrt{12}=\sqrt{3}$ . De andere rechthoekszijde meet $\sqrt{12}=2\sqrt{3}$ en is dus dubbel zo groot als de horizontale rechthoekzijde.
De zwarte driehoek is gelijkvormig met de rode en omdat de verticale rechthoekzijde gelijk is aan 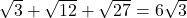$\sqrt{3}+\sqrt{12}+\sqrt{27}=6\sqrt{3}$ , moet de horizontale rechthoekzijde gelijk zijn aan de helft ervan , dus $3\sqrt{3}$ .
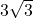Volgens de stelling van Pythagoras is het kwadraat van de zijde van het vierkant dan gelijk aan $(6\sqrt{3})^2+(3\sqrt{3})^2=135$
De gevraagde oppervlakte is dus 135.

Nootje 31

Geplaatst op 26 december 2022 door admin

Gegeven is $A=\begin{pmatrix} \cos x&-\sin x\\ \sin x &\cos x \end{pmatrix}$ . Bereken $A^{-50}$ voor $x=15^{\circ}$ .

Antwoord

Het zal zeker niet de bedoeling zijn om deze macht uit te rekenen.
Matrix A is eigenlijk de matrix voorstelling van het complex getal
$\cos x + i \sin x$
Gebruik van de formule van Lemoivre geeft
$A^{-50}=\begin{pmatrix} \cos -50x&-\sin -50x\\ \sin -50x &\cos -50x \end{pmatrix}$
Nu is $-50x=-750^{\circ}$ . We mogen altijd een veelvoud van $360^{\circ}$ bijvoegen zodat:
$A^{-50}=\begin{pmatrix} \cos -30^{\circ}&-\sin -30^{\circ}\\ \sin -30^{\circ} &\cos -30^{\circ} \end{pmatrix}$
Uitrekenen geeft
$A^{-50}=\frac{1}{2}\begin{pmatrix} \sqrt{3}&1\\-1&\sqrt{3}\end{pmatrix}$

Haberdasher puzzel

Geplaatst op 21 december 2022 door admin

In 1907 werd een bundeling van meer dan 100 puzzelproblemen gepubliceerd in het boek Canterbury puzzels van Henry Dudeney (1857 – 1930 . Dudeney was een Engels auteur en wiskundige met een voorliefde voor logische puzzels en wiskundige spelletjes. Eén van de meest bekende puzzels is de volgende: gegeven is een gelijkzijdige driehoek. Maak met slechts 3 insnijdingen van de driehoek 4 puzzelstukjes die kunnen omgevormd worden tot een vierkant met dezelfde oppervlakte als de gegeven driehoek.

Een mogelijke oplossing wordt gegeven als volgt:

Het midden van AB is D en van BC is het E.
Verleng AE to F zodat EF=EB.
G is het midden van AF.
Met G als middelpunt beschrijven we de boog AHF, waarbij H gelegen is op het verlengde van EB
Met E als middelpunt tekenen we de boog HI.
Construeer J op AC zodat IJ=BE
Teken IE
Teken uit D en J de loodlijnen op IE met voetpunten K and L.

Sangaku 10

Geplaatst op 16 december 2022 door admin

antwoord

Gevraagd wordt de totale oppervlakte vanher trapezium te berekenen.
De driehoeken met gegeven oppervlakten 32 en 50 zijn gelijkvormig. Hun oppervlakten verhouden zich als het kwadraat van de gelijkvormigheidsfactor. Bijgevolg is de gelijkvorrmgheidsfactor
$r=\frac{4}{5}$
Noteer dan $|AE|=4s$ en $|EC|=5s$ . Analoog $|DE|=4t$ en $|EB|=5t$ .
De 4 hoeken in E hebben allemaal eenzelfde sinus als overstaande hoeken of supplementaire hoeken. Noteer deze sinus door x.
Om de oppervlakte van een driehoek te berekenen, gebruiken we de formule: de helft van het product van twee zijden , vermenigvuldigd met de sinus van de ingesloten hoek.
Oppervlakte ADE= $\frac{1}{2}(4s*4t*x)=32$ . Dus is $stx=4$ .
De oppervlakte van AEB= $\frac{1}{2}(4s*5t*x)=10*stx=40$ Analoog is ook de oppervlakte van driehoek DEC gelijk aan 40.
De totale oppervlakte is dan 32 + 50 + 40 + 40 = 162.