Maandelijks archief: november 2022

Het getal van Champernowne

Geplaatst op door

Een 0, gevolgd door een komma en alle natuurlijke getallen op rij, noemt men het getal van Champernowne (Engels wiskundige 1912-2000).

  • Het is een irrationaal getal, want het kan niet geschreven worden als een quotiënt van twee gehele getallen.
  • Sommige irrationale getallen zijn transcendent ( zoals 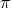\pi en e): ze zijn geen oplossing van een veeltermvergelijking met gehele coëfficiënten. Het getal van Champernowne is transcendent.
  • Sommige transcendente getallen zijn normaal. Elke eindige reeks van cijfers komt bij benadering even vaak voor als alle andere cijferreeksen van dezelfde lengte. David Champernowne heeft laten zien dat zijn getal normaal is  door aan te tonen dat niet alleen de cijfers 0 tot en met 9 even vaak voorkomen, maar ook alle combinaties van twee cijfers en alle combinaties van drie cijfers.

Het getal van Champernowne is een van de eerste geconstrueerde normale getallen. Hij bedacht het in 1933 en in 1937 bewees de Duitse wiskundige Kurt Mahler dat het transcendent was.

 

Een alien

Geplaatst op door

 

Op het bord staat de vergelijking

    \[x^3-19x^2+103x-247=0\]

Een alien komt binnen en roept: een drievoudige wortel! Net als wij heeft het buitenaards wezen 2 handen die onderling symmetrisch zijn. maar hoeveel vingers heeft hij (zij of het) aan elke hand?

antwoord

  • Als er een drievoudige wortel is dan is de vergelijking te schrijven onder de vorm (x-k)^3=0 of

        \[x^3-3kx^2+3k^2x-k^3=0\]

  • Nu is 247 geen derdemacht in ons tientallig stelsel, dus het gaat zeker al over een ander talstelsel. Noteer met b de basis van dat talstelsel.
  • De basis b moet even zijn, want onze alien heeft twee handen die symmetrisch zijn.
  • Verder moet b zeker groter zijn dan 10 want hij ziet het cijfer 9 staan.
  • Dus moet 3k=(19)_b of 3k=b+9. Hieruit volgt dat f=\frac{b+9}{3}.
  • Ook moet 3k^2=(103)_b of 3k^2=b^2+3. Als we hierin k vervangen door \frac{b+9}{3} vinden we 2b^2-18b-72=0. Bijgevolg is k=12 of k=-3. Dit laatste kan uiteraard niet.
  • Controleer nog of k ^3=(247)_b met b=12. Dit klopt.
  • Het buitenaards wezen heeft 6 vingers aan elke hand.