Overdekkingen van het vlak

Geplaatst op 27 augustus 2022 door admin

We gaan op zoek naar regelmatige bedekkingen van het vlak: dit zijn bedekkingen met regelmatige n-hoeken met alle dezelfde lengte als zijde. Het vlak is dan de unie van al die veelhoeken en de doorsnede van twee veelhoeken is ledig, ofwel een punt ofwel een zijde. We eisen ook dat de hoekpunten gelijkwaardig zijn, dus dat in een punt steeds dezelfde veelhoeken in dezelfde aantallen en in dezelfde volgorde voorkomen. Noteren we met $q$ het aantal verschillende veelhoeken in een bepaald knooppunt.

De waarde van een hoek van een regelmatige n-hoek is

$\frac{n-2}{n}180^{\circ}$

Neem eerst het geval $q=1$ . Noteer met m het aantal veelhoeken in een knooppunt. Dan moet $m.\frac{n-2}{n}180^{\circ}=360^{\circ}$ . Hieruit volgt dat $m(n-2)=2n$ of $(m-2)(n-2)=4$ . Hierbij zijn uiteraard m en n natuurlijke getallen. De enige oplossingen zijn:

$(m,n)=(6,3), (m,n)=(3,6), (m,n)=(4,4)$

Dus drie zeshoeken, zes driehoeken of vier vierkanten.

Neem nu $q=2$ ( we spreken dan van Archimedische vlakvullingen) en stel dat er a regelmatige m-hoeken en b regelmatige n-hoeken samenkomen, dan moet $a.\frac{m-2}{m}180^{\circ}+b.\frac{n-2}{n}180^{\circ}=360^{\circ}$ of

$a+b=2(\frac{a}{m}+\frac{b}{n}+1)$

Omdat $\frac{a}{m}+\frac{b}{n}>0$ zal $a+b\geq3$ . Omdat de klenst mogelijke hoek van een regelmatige veelhoek $60^{\circ}$ is, zal $a+b\leq 6$ . Bijgevolg geldt:

$3 \leq a+b \leq 6$

Geval 1: $a=1$ en $b=2$ , dan is $n=\frac{4m}{m-2}$ en zijn de enige natuurlijke oplossingen: $(m,n)=(3,12)$ en $(m,n)=(4,8)$ . De oplossing $(m,n)=(6,6)$ hebben we al en $(m,n)=(10,5)$ geeft geen regelmatige overdekking. De twee oplossingen geven we volgende typering: $3,12^2$ ( 1 driehoek en 2 twaalfhoeken) en $4,8^2$ (1 vierkant en 2 achthoeken).

Geval 2: $a=1$ en $b=3$ , dan is $n=\frac{3m}{3m-2}$ en is de enige natuurlijke oplossing: $(m,n)=(4,4)$ en die hebben we al gehad bij $q=1$ .

Geval 3: $a=1$ en $b=4$ , dan is $n=\frac{8m}{m-2}$ en zijn de enige natuurlijke oplossingen: $(m,n)=(6,3)$ . Typering: $6,3^4$ ( een zeshoek en 4 driehoeken)Geval 4: $a=2$ en $b=2$ , dan is $n=\frac{2m}{m-2}$ en zijn de enige natuurlijke oplossingen: $(m,n)=(3,6)$ , $(m,n)=(4,4)$ en $(m,n)=(6,3)$ . De oplossing $(m,n)=(4,4)$ hebben we al. Bovendien geven $(6,3)$ en $(3,6)$ dezelfde oplossing.Rest nog het geval $6^2,3^2$ (2 zeshoeken en 2 driehoeken).

Geval 5: $a=2$ en $b=3$ , dan is $n=\frac{6m}{3m-4}$ en is de enige natuurlijke oplossing: $(m,n)=(4,3)$ . Type $4^2,3^3$ ( twee vierkanten en drie driehoeken). We verfijnen de typering: links de overdekking $(3,3,3,4,4)$ en rechts $(3,3,4,3,4)$ .

Neem nu $q=3$ en stel dat er a regelmatige m-hoeken, b regelmatige n-hoeken en c regelmatige p-hoeken samenkomen, dan moet $a.\frac{m-2}{m}180^{\circ}+b.\frac{n-2}{n}180^{\circ}+c.\frac{p-2}{p}180^{\circ}=360^{\circ}$ of

$a+b+c=2(\frac{a}{m}+\frac{b}{n}+\frac{c}{p}+1)$

Waarbij $3\leq a+b+c<6$ zodat voor $(aub,c)$ volgende mogelijkheden moeten worden onderzocht: $(1,1,1),(2,1,1),3,1,1)$ en $(2,2,1)$ .

Geval 1: $(a,b,c)=(1,1,1)$ . Dan is $p=\frac{2mn}{mn-2m-2n}$ . Onderzoek van verschillende mogelijkheden geeft $(m,n,p)=(5,10,5),(5,20,4),(6,12,4),\\(8,8,4),(12,12,3),(15,10,3),(18,9,3),(24,8,3),(42,7,3)$ . Enkel $(m,n,p)=(6,12,4)$ levert een nieuwe bestaande overdekking. We krijgen een zeshoek, een twaalfhoek en een vierkant in elk knooppunt.

Geval 2: $(a,b,c)=(2,1,1)$ . Enkel $(m,n,p)=(4,6,3)$ levert een nieuwe bestaande overdekking. We krijgen twee vierkanten , een zeshoek en een driehoek in elk knooppunt. 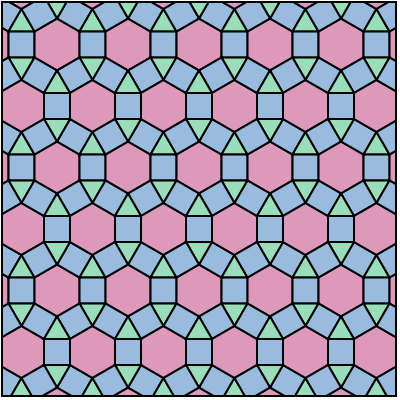Geval 3: $(a,b,c)=(3,1,1)$ . Deze combinatie levert geen nieuwe oplossingen.

Geval 4: $(a,b,c)=(2,2,1)$ . Deze combinatie levert geen nieuwe oplossingen.

Situaties met $q=4,5$ of $6$ kunnen niet voorkomen want $60+90+108+120=378>360$ .

Fascisme

Geplaatst op 19 augustus 2022 door admin

Op 23 maart 1919 maakt Benito Mussolini in Milaan bekend dat hij een nieuwe beweging wil oprichten: de Fasci Italiani de Combattimento.

De naam Fasci verwijst naar de Romeinse fasces, symbool voor macht, samenhorigheid en eenheid.

De aanleiding hiertoe is de anarchie waarin Italië verkeert na het einde van WO1. Op 6 juni maakt Mussolini zijn doelen bekend in zijn krant Il Popolo d’Italia : een achturige werkdag, betere sociale voorzieningen, schoolplicht, confiscatie van kerkelijke eigendommen, verdeling van de grond onder veteranen, verdrijving van de elite en vooral een krachtige buitenlandse politiek.

Zijn aanhang groeit snel en overal ontstaan knokploegen die eigenhandig Mussolini willen helpen. Een golf van geweld overspoelt Italië en Mussolini beweert dat hij de enige leider ( duce) is die de orde kan herstellen en Italië weer groot kan maken.

In mei 1925 neemt hij deel aan de verkiezingen en haalt 35 van de 275 zetels, een reden om 5 maand later zijn beweging om te vormen tot een politieke partij: de Partite Nazionale Fascista (PNF). Een jaar later marcheert hij met 25000 volgelingen naar Rome. Koning Victor Emmanuel 3 wil verder geweld en een eventuele burgeroorlog voorkomen, en vraagt Mussolini een nieuwe regering te vormen onder diens leiding.

Construeerbare getallen

Geplaatst op 17 augustus 2022 door admin

In deze tekst onderzoeken welke we getallen er construeerbaar zijn met de klassieke constructieapparaten, passer en liniaal. Verder bestuderen we ook de structuur van de verzameling van alle construeerbare getallen. We komen zo tot een modern algebraïsch bewijs van de onmogelijkheid om met passer en liniaal een kubus te verdubbelen. Dit is een welbekend probleem uit de oude Griekse meetkunde. Zo zien we dat algebra en meetkunde enerzijds en oude en moderne wiskunde anderzijds erg nauw samenlopen.

Python: de zeef van Eratosthenes

Geplaatst op 13 augustus 2022 door admin

De zeef van Eratosthenes (Bibliothecaris van de bibliotheek van Alexandrië rond 240 v.C.) is een algoritme om priemgetallen te bepalen kleiner dan een gegeven getal n:

Maak een geordende lijst van alle getallen van 2 tot n.
Neem het kleinste getal in deze lijst en schrap alle veelvouden van dit getal ( het getal zelf niet!).
Neem het volgende getal in de lijst en doe hiervoor hetzelfde.

Een programma in Python geeft bijvoorbeeld alle priemgetallen kleiner dan 50

Uitleg:

Neem een lijst van lengte n en zet op elke plaats de boolse waarde True.
Begin met p=2 en zet alle veelvouden van 2 in de lijst op False. Begin met het eerste veelvoud van 2 na 2 zelf: dat is 2*2.
Neem dan p=3 en zet alle veelvouden van 3 op False, beginnend met 3*3
(want alle vroegere veelvouden zijn sowieso al op False gezet.
Doe zo verder zolang p*p kleiner is dan de gegeven waarde n.

Nootje 28

Geplaatst op 9 augustus 2022 door admin

Toon aan dat de som van de breuken $\frac{a-b}{1+ab},\frac{b-c}{1+bc},\frac{c-a}{1+ac}$ gelijk is aan hun product.

Spoiler

Noem die breuken A,B en C. Je zou A+B+C en A.B.C kunnen uitrekenen maar dat ziet er niet leuk uit…
De vorm van de breuk doet me echter denken aan de formule van de tangens van een verschil:
Vermits a,b en c reële getallen zijn bestaan er getallen $\alpha,\beta ,\gamma$ met $-\frac{\pi}{2}<\alpha,\beta,\gamma<\frac{\pi}{2}$ zodat $a=\tan \alpha,b=\tan \beta$ en $c=\tan \gamma$ .
We moeten dan bewijzen dat $\tan(\alpha-\beta)+\tan(\beta-\gamma)+\tan(\gamma-\alpha)=\tan(\alpha-\beta)*\tan(\beta-\gamma)*\tan(\gamma-\alpha)$ .
Of als $x+y+z=0$ , dat $\tan x+\tan y+\tan z=\tan x*\tan y*\tan z$ .
Dit is vrij simpel: begin met het linkerlid en vervang z door $-(x+y)$ .

Wiskunde is leuk

Maandelijks archief: augustus 2022

Overdekkingen van het vlak

Fascisme

Construeerbare getallen

Python: de zeef van Eratosthenes

Nootje 28