De klok

Geplaatst op 27 maart 2022 door admin

Kunnen de drie wijzers van een uurwerk onderling twee aan twee hoeken van 120 graden vormen?

Noteer het tijdstip als x. Dit is een reëel getal. De kleine wijzer staat dan op 30x mod 360. graden, want na 1 uur heeft deze wijzer 30 graden afgelegd. De grote wijzer staat dan op 360x mod 360 graden, vermits er 60 minuten in een uur zijn. Omdat er 60 seconden in een minuut zijn , zal tenslotte de secondewijzer op 21600x mod 360 graden staan.
Het vraagstuk herleidt zich tot een volgend stelsel (telkens mod 360 genomen):
$30x-360x=120$

$360x-21600x=120$

$21600x-30x=120$
Het kan ook het volgende stelsel geven:
$360x - 30x=120$

$21600x-360x=120$

$30x-21600x=120$
We bespreken enkel het eerste stelsel; het tweede geval verloopt analoog.
Na vereenvoudiging krijgen we :
$x=\frac{4}{11}(\mod \frac{12}{11})$

$x=\frac{1}{177}(\mod \frac{3}{177})$

$x=\frac{8}{719}(\mod \frac{12}{719})$
Dus
$x=\frac{4}{11}(1+3k)=\frac{1}{177}(1+3l)=\frac{4}{719}(2+3m)$
Maar dan moet
$4.177.719(1+3k)=11.719(1+3l)$
Dis is onmogelijk want het eerste lid is een drievoud en het tweede niet!
De drie wijzers kunnen dus nooit twee aan twee een hoek van 120 graden vormen.

3n+1 via Python

Geplaatst op 20 maart 2022 door admin

Het 3n+1 probleem is wel bekend. Als onderdeel van een project rond onderzoeksvaardigheden heeft Frederik Nijs, leerling van 5WEWIc, uit het Sint-Jozefcollege Aarschot een Python programma hiervoor gemaakt.

Omzetting mijlen naar kilometer

Geplaatst op 17 maart 2022 door admin

1 mijl( = 1 mi ) is 1,609344 km, wat dicht bij het gulden getal $\varphi =1,618$ ligt. De waarde van $\varphi$ wordt benaderd door de verhouding van twee opeenvolgende getallen in de rij van Fibonacci. Daarom kan je voor de omzetting van mijlen naar kilometer en omgekeerd gebruik maken van opeenvolgende Fibonacci getallen, met vrij grote nauwkeurigheid.

Priemtweelingen

Geplaatst op 11 maart 2022 door admin

Een paar opeenvolgende priemgetallen waarvan de afstand 2 is, noemen we een priemtweelingen. Buiten de eerste priemtweelingen 3-5 vinden we bijvoorbeeld ook 5-7, 11-13, 17-19,… Ze ontstaan allemaal (behalve 3-5), door vertrekkend van 5-7, een translatie uit te voeren over 6 eenheden. Dit is logisch want een priemgetal is altijd van de vorm 6k+1 of 6k-1.

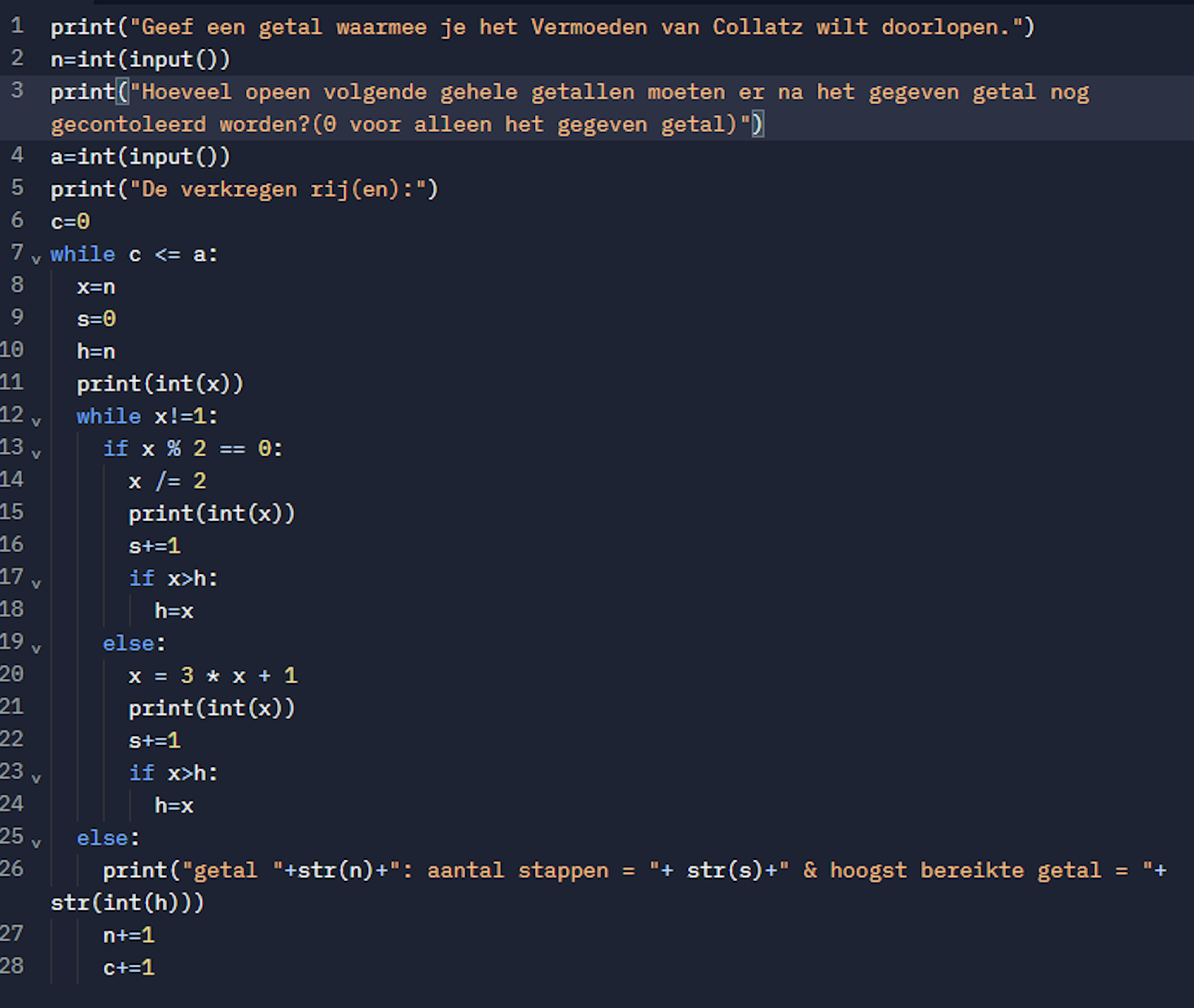
Een Python programma om alle priemtweelingen kleiner dan 1000 te bepalen:
De output:

Een paar ‘leuke ‘ eigenschappen, die zeer eenvoudig te bewijzen zijn:

Een priemtweelingen heeft een symmetriemidden dat steeds een 6-voud is.
De som van twee elementen van een priemtweelingen is steeds een 12-voud.
De afstand voor de overeenkomstige elementen van twee priemtweelingen is steeds een 6-voud.
De afstand van het grootste getal van de kleinste priemtweeling tot het kleinste getal van de grootste priemtweelingen is een 6-voud min 1.
Er bestaat geen grootste priemtweeling.

Opgave 34: Een integraal…

Geplaatst op 4 maart 2022 door admin

Bereken $A=\int_0^{\frac{\pi}{4}} ln(1+tan x) dx$

Gewone methoden werken hier niet.
Als een functie f gedefinieerd is op $\left[a,b\right]$ dan kan je de functie spiegelen rond de middelloodlijn van dit lijnstuk en bekom je de functie $g(x)=f(a+b-x)$ .
Uit de definitie van de bepaalde integraal volgt dan dat $\int_a^bf(x) dx=\int_a^b g(x) dx$ .
Passen we dit toe op de opgave , dan krijgen we: $A=\int _0^{\frac{\pi}{4}} ln(1+tan(\frac{\pi}{4}-x)) dx$ .
Nu is $tan(\frac{\pi}{4}-x)=\frac{1-tan x}{1+tan x}$ .
Zodat $A=\int _0^{\frac{\pi}{4}} ln\Big( \frac{2}{1+ tan x}\Big) dx$ .
Gebruikmakend van de rekenregels voor logaritmen, volgt hieruit dat $A=\int _0^{\frac{\pi}{4}} ln(2) dx -A$ .
Bijgevolg is $A=\frac{\pi}{8} ln(2)$ .

Wiskunde is leuk

Maandelijks archief: maart 2022