Maandelijks archief: oktober 2020

necker kubus

Geplaatst op door

De Necker kubus is vernoemd naar de Zwitserse kristallograaf Louis Necker (1786-1861)
Het is een lijntekening van een kubus in perspectief. Het is niet mogelijk te zeggen welke zijde van de kubus zich aan de voorkant bevindt. Twee mogelijkheden: 

 

Sangaku 2

Geplaatst op door

Dit probleem komt uit de verzameling Siri Shinpen van Saito Gigi (1816-1889). Het werd door Nakasone Munekuni voorgesteld in 1856 en opgehangen in de Haruna schrijn in Haruna.

Antwoord

  • Te bewijzen is dat de groene oppervlakte en de oranje oppervlakte gelijk zijn.
  • De groene oppervlakte  bestaat uit 2 cirkels (2\pi r^2) en n cirkelsectoren. De oppervlakte van een cirkelsector is \frac{1}{2}r^2\alpha.
  • Als we al de oppervlaktes van die sectoren optellen vinden we \frac{1}{2}r^2S met S de som van al de hoeken van de getekende veelhoek. Dus is S=(n-2)\pi. 
  • De groene oppervlakte is dus \frac{n+2}{2}\pi r^2.
  • De oranje oppervlakte bekomen we door n cirkels te verminderen met een deel van de groene oppervlakte: \pi nr^2-\frac{n-2}{2}\pi r^2 en na vereenvoudiging is dat ook \frac{n+2}{2}\pi r^2.

Spidron

Geplaatst op door

De Spidron is een vlakke figuur die is opgebouwd uit twee afwisselende reeksen van gelijkbenige driehoeken:

De eerste spidron werd ontwikkeld door Dániel Erdély in 1979, als een taak voor Erno Rubik in zijn design klas aan de Hongaarse Universiteit .

Andere  mooie ontwerpen: 

Pythagoras

Geplaatst op door

Vraag iemand wat hij nog kent uit de wiskunde, dan heb je veel kans dat de naam Pythagoras voor de dag komt.

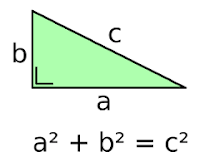Vooreerst: de stelling  werd reeds  lang toegepast voor er zelfs sprak was van Pythagoras. De Babyloniërs, Egyptenaren en Chinezen kenden deze eigenschap reeds lang. Op verschillende Babylonische kleitabletten komen vraagstukken voor, waarin een zijde van een rechthoekige driehoek berekent wordt uit de twee andere zijden.  Zij beschikten zelfs over tabellen van Pythagoras getallen ( gehele getallen die voldoen aan de stelling hierboven). Typisch bij die preredenerende wiskunde is dat geen enkel bewijs werd aangetroffen. De formules werden ook niet in een algemene vorm opgeschreven, maar onmiddellijk toegepast.

Voor bewijzen in de wiskunde moeten we wachten tot de Grieken op de voorgrond treden. Voor de eerste keer in de geschiedenis heeft de mens behoefte de wereld en haar verschijnselen te verklaren met behulp van het zuivere intellect.  Zo zou bijvoorbeeld de wiskundige Thales omstreeks 600 voor Christus voor het eerst het aspect bewijzen naar voor brengen in zijn werk.

Het is echter Pythagoras die we de eerste exacte wetenschappelijke onderzoeker kunnen noemen. Hij was niet de ontdekker van de naar hem genoemde stelling, maar hij was wel de eerste die een algemeen meetkundige bewijs gaf. Hij  was  de  eerste  wiskundige die  de  wiskunde  bestudeerde  als   theorie  en  niet  als praktische toepassing.   De intellectuele  sprong van 5 mensen,  5 boten, enz. naar  het  abstracte  getal 5 was  een  grote  gebeurtenis,  ook   al  is  dat  voor   ons  volkomen  normaal.

Pythagoras werd geboren rond 570 v. Chr. op het Griekse eiland Samos. Hij groeide op op Samos en reisde veel met zijn vader en bezocht zo de Griekse filosoof en wiskundige Thales en woonde lezingen bij van Anaximander, een leerling van Thales. Hij bezocht ook Egypte en tijdens de oorlog tussen Egypte en Perzië werd hij gevangengenomen en naar Babylon gebracht. Rond 520 v. Chr. keerde hij terug naar Samos. Vlak daarna ging hij naar Zuid-Italië en stichtte zij Pythagoreïsche school in Croton.

Pythagoras’ groep, de Pythagoreeërs, was een soort sekte waar religie en wiskunde hand in hand gingen. De Pythagoreeërs bestonden uit twee groepen: de eerste groep de mathematikoi , woonde bij en werd onderwezen door Pythagoras. De groep moest ethisch leven, het pacifisme aanhangen en de ‘ware aard van de werkelijkheid’ bestuderen: getallen of wiskunde. De tweede groep waren  de akousmatikoi, die in hun eigen huis woonden en alleen overdag naar de school kwamen.

Maar niet alles was wiskunde. De  Pythagoreeërs geloofden ook in zielsverhuizing en reïncarnatie.    

In 508 v. Chr. werd de Pythagoreïsche gemeenschap aangevallen door Cylon, een edelman uit Croton. Pythagoras vluchtte naar Metaponte en overleed ongeveer 8 jaar later. Na zijn dood splitste de groep zich op in een wiskundige en een religieuze tak.

Over goniometrie

Geplaatst op door

Het woord goniometrie of trigonometrie komt van twee Griekse woorden: trigonon(driehoek) en metro(maat).

Zo’n 3000 jaar geleden kenden de oude Babyloniërs een vorm van goniometrie en van hen kwam het idee van 360^\circ. Ze gaven ons zestig minuten in een graad en zestig seconden in een minuut.

Ook de grieken gebruikten al ver gevorderde goniometrie. Euclides en Archimedes ontwikkelden stellingen, weliswaar meetkundig met goniometrische equivalenten. De eerste goniometrische tabel (Tōn en kuklōi eutheiōn (Of Lines Inside a Circle) is waarschijnlijk gemaakt door Hipparchus van Nicaea door sommigen de ‘vader van de goniometrie genoemd.

De tabel was een hulpmiddel bij het oplossen van driehoeken maakte gebruik van koorden en de formule

    \[\text{koorde}(\alpha)=2r \sin \frac{\alpha}{2}\]

De Indiase wiskundige Aryabhata ( 476-550 BC) ontwikkelde de verhoudingen van sinus  ( overstaande rechthoekzijde tot schuine zijde) en cosinus ( aanliggende rechthoekzijde tot schuine zijde). In zijn werk Saan ook de oudste bewaard gebleven sinustabellen.

In de zevende eeuw maakte de Indiase wiskunde Bhaskara een vrij nauwkeurige formule om de sinus van x ( in radialen) uit te rekenen zonder tabel:

    \[\sin x=\frac{16x(\pi-x)}{5\pi^2-4x(\pi-x)}\]

Deze ideeën kwamen via Perzië naar  het westen. Al-Khwarizmi maakte in de negende eeuw goniometrische tabellen voor sinus, cosinus en tangens. Een eeuw later gebruikten islamitische wiskundigen de volledige ‘bubbel van 6’ ( sinus, cosinus, tangens, secans, cosecans en cotangens) en zij hadden tabellen voor toenames met een kwart graad, die tot 8 decimalen nauwkeurig waren.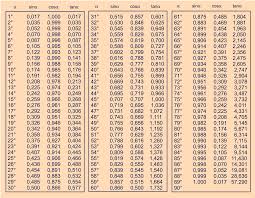

Nu kent de goniometrie vooral toepassingen in de landmeetkunde en de navigatie