Maandelijks archief: september 2020

Foutenverbeterende codes

Geplaatst op door

Stel, je wilt de  boodschap HELLO doorgeven van de ene computer aan de andere. Dat kan bijvoorbeeld door gebruik te maken van een tabel die de boodschap omzet in binaire tekens. De ontvanger kan de boodschap dan decoderen met dezelfde tabel. Een voorbeeld van zo een tabel is de ASCII-tabel: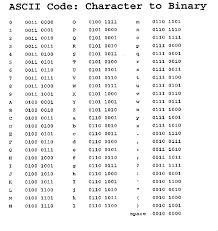

Maar er kunnen  fouten  bij het verzenden optreden; zo kan de letter H = 0100 1000 ontvangen worden als 01001010, wat de letter J geeft!

Een manier om te weten of er een fout is opgetreden, is het toevoegen van een extra bit aan de boodschap, het zogenaamde pariteitsbit. Voor een even pariteit code zorgen we ervoor dat het aantal 1-en altijd even is.

Zo wordt H = 0100 1000 0 ( de laatste nul is het pariteitsbit dat ervoor zorgt dat het totaal aantal enen even is). Als je nu 0100 1010 0 ontvangt, weet je dat er een fout in de verzending zit omdat er een oneven aantal enen staat. We spreken van een fout ontdekkende code : we weten dat er minstens 1 foute bit in de boodschap zit, maar we kunnen die niet verbeteren omdat we niet weten waar de fout zit

Het was de Amerikaanse wiskundige Richard Hamming (1915-1998) die een oplossing vond voor dit probleem.

Om een 4 bits rij d_1d_2d_3d_4 te coderen gebruikte hij 3 cirkels: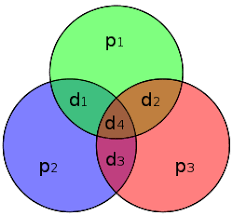

Hij plaatste de gegeven bits zoals hierboven gegeven en voegde er dan de even pariteitsbits p_1,p_2 en p_3 aan toe. Voor 1001 wordt de code dan 1001001. Als er nu een fout zit in het verzenden en er wordt 1011001 ontvangen, dan kan je door de pariteit te controleren in de drie cirkels zien dat de fout zit in de blauwe en rode,  maar niet in de groene cirkel. Dus bit d_3 was fout en de verzonden boodschap was dan 1001!

Dit is fouten verbeterende code. men noemt het de (7,4) Hamming code. De notatie (7,4) betekent dat elke 4 bits informatie gecodeerd worden als een 7 bit rijtje.

Pi met wortels

Geplaatst op door

Hoe kan je pi benaderen door middel van wortels? Bekijk volgende  mogelijkheid: de oppervlakte van een cirkel met straal 1 benaderen we door het gemiddelde te nemen van de oppervlaktes van een ingeschreven regelmatige achthoek en een omgeschreven regelmatige zeshoek.

  • Neem een omgeschreven zeshoek :
    om de oppervlakte te berekenen nemen we zes keer de oppervlakte van OAB. De hoogte OM van die driehoek is 1. De basis AB is 2*\tan 30^\circ=\frac{2\sqrt{3}}{3}. Bijgevolg is de oppervlakte van de zeshoek gelijk aan 2\sqrt{3}.
  • Neem vervolgens een ingeschreven regelmatige achthoek:
    de oppervlakte is gelijk aan acht keer de oppervlakte van driehoek OAB. De oppervlakte van die driehoek is gelijk aan \frac{1}{2}*1*1*\sin 45^\circ=\frac{\sqrt{2}}{4}, zodat de oppervlakte van de achthoek gelijk is aan 2\sqrt{2}.
  • Het gemiddelde van die twee oppervlaktes is dan \sqrt{2}+\sqrt{3}.
  • Aldus is \pi \approx \sqrt{2}+\sqrt{3}\approx 3.14626436994

Kwadraten in de driehoek van Pascal

Geplaatst op door

In de driehoek van Pascal kan je veel verbanden vinden. Vandaag gaan we op zoek naar kwadraten.

  • Kijk naar de derde kolom van de driehoeksgetallen 1,3,6,10,… en tel daar de elementen twee per twee op en je vindt de rij 4,9,16,25,… Hoe kan je dit verklaren?  De som van de elementen is altijd van de vorm

        \[\binom{n}{2}+\binom{n+1}{2}\]


    Uitrekenen geeft \frac{1}{2}n(n-1)+\frac{1}{2}n(n+1)=n^2.
  • Kijk naar de vierde kolom 1,4,10,20,35,56,…en bereken het verschil van de derde en de eerste, de vierde en de tweede enz. , dan vorm je de rij 9,16,25,… Verklaring?

        \[\binom{n+2}{3}-\binom{n}{3}\]

    Uitrekenen met de formule van Stiffel geeft: \Big(\binom{n+2}{3}-\binom{n+1}{3}\Big)+\Big(\binom{n+1}{3}-\binom{n}{3}\Big)=\binom{n+1}{2}+\binom{n}{2}=n^2.

Stelling van Ptolemaeus

Geplaatst op door

De kans, dat 4 willekeurig gekozen punten in het vlak, op 1 lijn of 1 cirkel liggen is erg klein. Er moeten dus  wel speciale voorwaarden zijn om dit te doen gebeuren.  Zo een voorwaarde wordt gegeven in de stelling van Ptolemaeus:

Voor 4 willekeurige punten A,B,C en D in het vlak, geldt

    \[AB.CD+AD.BC \geq AC.BD\]

Er treedt gelijkheid op als de punten collineair of concyclisch zijn .

Enkele gevolgen:

  • Als ABCD een koordenvierhoek is en ABC een gelijkzijdige driehoek, dan is BD=AD+CD.
  • Als ABCD een koordenvierhoek is en de hoeken in B en D zijn recht, dan is BD=AC.\sin A ( schrijf de hoek A als som van twee hoeken en pas de domformule voor \sin(x+y) toe)

Pariteit van een permutatie

Geplaatst op door

Elke permutatie kan geschreven worden als het product ( samenstelling) van transposities. Een transpositie of omwisseling is een twee-cykel, zoals bijvoorbeeld (12).

Dit product kan op verschillende manieren tot stand komen, maar het is wel zo dat het aantal transposities dat je nodig hebt, steeds hetzelfde is. Als dat aantal even is , spreken we van een even permutatie. Als het aantal oneven is , spreken we van een oneven permutatie.  Dit noem je de pariteit van de permutatie

Een voorbeeldje van een oneven permutatie:

    \[(1234) =(14)(13)(12)\]

    \[(1234)=(12)(23)(34)\]

Let op de volgorde! Zoals bij de samenstelling , werken we van achter na voor. Nog een paar voorbeelden met afbeelding:

 

is een even permutatie, want de permutatie is te schrijven als (16)(15)(13)(28)(27)(24).

is een oneven permutatie, want de permutatie is te schrijven als (14)(32)(35)