Neem willekeurig 4 getallen uit de verzameling A={1,2,3,4,5,6,7}. Hoe groot is de kans dat hun som even is?
Antwoord
Maandelijks archief: juli 2020
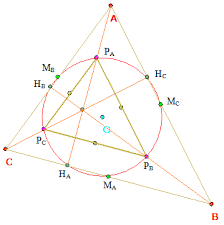
Middendriehoek
De middendriehoek van een driehoek ABC is de driehoek SRQ, gevormd door de middenparallellen van de gegeven driehoek.
Enkele eigenschappen:
- De oppervlakte van de middendriehoek is
van de oppervlakte van de gegeven driehoek. - De omtrek van de middendriehoek is
van de omtrek van de gegeven driehoek. - De middendriehoek is gelijkvormig met de gegeven driehoek: de middendriehoek is het beeld van ABC onder een homothetie met centrum het zwaartepunt van ABC en als factor
. - De middendriehoek en driehoek ABC hebben hetzelfde zwaartepunt.
- Het hoogtepunt van de middendriehoek valt samen met het middelpunt van de omgeschreven cirkel van driehoek ABC.
- De voetpunten van de hoogtelijnen van driehoek ABC liggen op de omgeschreven cirkel van de middendriehoek.
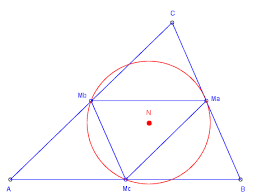
- De omgeschreven cirkel van de middendriehoek is de negenpuntscirkel van ABC ( de cirkel door de middens van de zijden, de voetpunten van de hoogtelijnen en de middens van de lijnsegmenten van uit de hoekpunten naar het hoogtepunt ).
- En dan nog deze afsluiter: bedenk zelf maar de stelling!
Een meetkundige parel
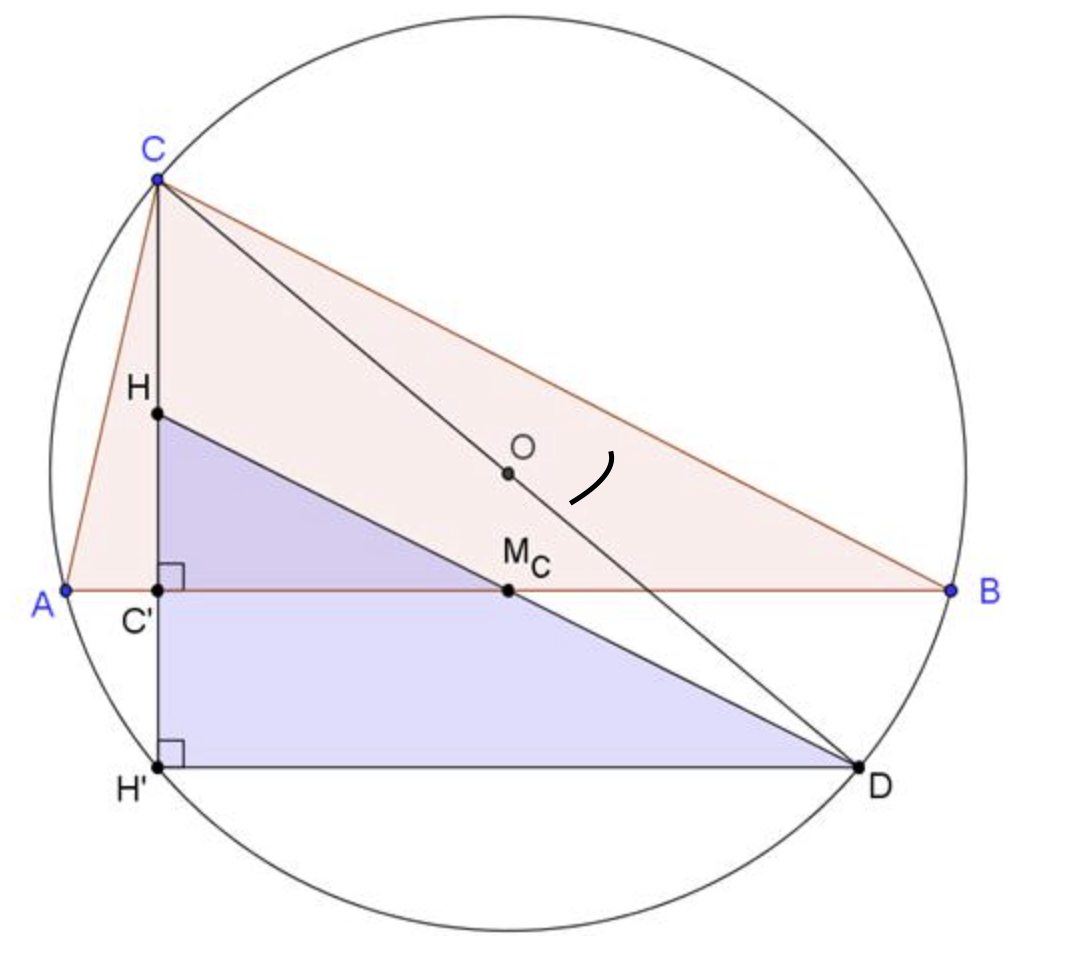
Onlangs vond ik volgende stelling die ik helemaal niet kende. Een echt pareltje: De spiegelbeelden van het hoogtepunt van een driehoek ABC rond de zijden en rond de middens van de zijden liggen op de omgeschreven cirkel van ABC.
H’ is het spiegelbeeld van H (hoogtepunt) rond de zijde AB en CD is een middellijn van de omgeschreven cirkel.
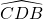is een rechte hoek, als omtrekshoek op een halve cirkel. Omdat AH loodrecht op BC staat, zijn BD en AH evenwijdig.- Analoog is AD ook evenwijdig met BH.
- Dus is AHBD een parallellogram.
- Omdat de diagonalen van een parallellogram elkaar midden doordelen is
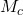het midden van AB en dus is D inderdaad het spiegelbeeld van H bij een puntspiegeling rond het midden van B. - Omdat HC’=C’H’ is
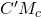de middenparallel van driehoek HH’D en staat DH’ loodrecht op CC’ omdat DH’ evenwijdig is met 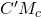. - Dus is
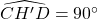en wegens de eigenschappen van omtrekshoeken ligt dus H’ op de omgeschreven cirkel van driehoek ABC.
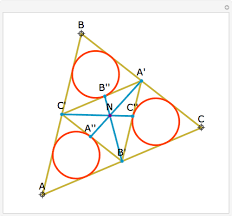
Isogonaal toegevoegde punten
Om het isogonaal toegevoegd punt van P te berekenen, construeert men het snijpunt van de spiegelbeelden van AP, BP en CP ten opzichte van de respectievelijke bissectrices van de hoeken A,B en C. Het is duidelijk dat de hoeken CAP en QAB gelijk zijn. analoog zijn ook ABP en QBC gelijk en BCP en QCA.
Een andere mogelijke constructie werkt met de voetpuntsdriehoek: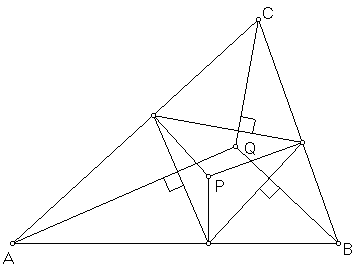 
Men tekent de loodlijnen vanuit P op de drie zijden van de driehoek. Hun voetpunten vormen de voetpuntsdriehoek. Construeer nu snijpunt Q van de loodlijnen uit A,B en C op de zijden van de voetpuntsdriehoek. Dan zijn P en Q isogonaal toegevoegd.
Een paar voorbeelden:
- Het middelpunt van de ingeschreven cirkel is isogonaal toegevoegd aan zichzelf.
- Het hoogtepunt van een driehoek en het middelpunt van zijn omgeschreven cirkel zijn isogonaal toegevoegd.
Raadsel
De leraar wiskunde stelt volgende vraag op het proefwerk aan zijn leerlingen: ‘Zoek het getal dat ik in gedachten heb. Het getal is gelegen tussen 13 en 1300. En jullie mogen drie vragen stellen over dit getal, waar ik met ja of nee op antwoord, en dan moeten jullie dit getal kunnen bepalen.’
Eerste vraag van de leerlingen: ‘Is het getal kleiner dan 500?’
De leraar antwoordt, maar hij liegt.
Tweede vraag van de leerlingen: ‘Is het getal een volkomen kwadraat?’
De leraar antwoordt, maar hij liegt weer.
Derde vraag van de leerlingen: ‘Is het getal een volkomen derdemacht?’
De leraar antwoordt en nu spreekt hij de waarheid.
De leerlingen beginnen nu te rekenen, maar ze zitten nog vast.
De leraar staat hen dan toe nog een vierde vraag te stellen.
Vierde vraag: ‘Is het laatste cijfer van dat getal een 2?’
De leraar antwoordt en spreekt weer de waarheid.
Eén van de leerlingen heeft het nu gevonden. ‘Dit is het getal’, zegt hij. Het is natuurlijk verkeerd.
Welk is het getal dat de leraar in gedachten had?
Antwoord