Maandelijks archief: juli 2020

Vierkwadraten stelling

Geplaatst op door

Elk priemgetal, gelijk aan 1 modulo 4, kan geschreven  worden als som van twee kwadraten. Dat een getal als som van twee kwadraten
geschreven kan worden is niet vanzelfsprekend. Bij een getal dat 3 (mod 4) is kan dat bijvoorbeeld niet. Daarentegen bleek dat wel elk getal getal te schrijven is als som van vier kwadraten.

Elk positief geheel getal kan geschreven worden als som van 4 kwadraten van gehele getallen.

    \[n=x_1^2+x_2^2+x_3^2+x_4^2\]

Deze stelling was al gekend door Diophantus; Euler heeft 40 jaar gezocht naar een bewijs ervan, maar het was Joseph-Louis Lagrange ( 1736 – 1813)  die in 1772 het eerste bewijs formuleerde.

Het kan zelfs in veel gevallen met drie kwadraten. Legendre ( 1752 – 1833) beweerde dan elk getal, tenzij van de vorm 4^k(8m+7) , te schrijven is als som van drie kwadraten.

Er bestaat zelfs een mogelijkheid  om  het totaal aantal manieren  te berekenen, waarop een gegeven positief geheel getal n  kan worden geschreven als de som van vier kwadraten. Als n oneven is moet je 8 keer de som van zijn delers nemen en als n even is 24 keer de som van zijn oneven delers. Merk hierbij op dat (x_1,x_2,x_3,x_4) geordend is en dat we gehele oplossingen zoeken ; dus ook rekening houden met negatieve getallen.

Nog een raadseltje

Geplaatst op door

De pastoor geeft zijn parochieassistente een probleempje om op te lossen: “Er zijn drie parochianen waarvan het product van de ouderdommen gelijk is aan 2450. De som van hun ouderdommen is het dubbel van jouw leeftijd.” De assistente zegt: “Ik weet het nog niet.” Dan zegt de pastoor: “De drie parochianen zijn alle drie jonger dan ik.’ “Nu weet ik het,” roept de parochieassistente. Welke zijn de leeftijden van de drie parochianen?

Antwoord

  • Noem de parochianen a, b en c en de assistente x. We gaan ervan uit dat de leeftijden allemaal natuurlijke getallen zijn.
  • 2450=2*5*5*7*7. We maken een tabel van de mogelijkheden waarvoor abc = 2450 en berekenen tegelijkertijd ook x ( de helft van  a + b + c). We gebruiken enkel ‘echte’ leeftijden, dus niet bvb 1225 of zo.

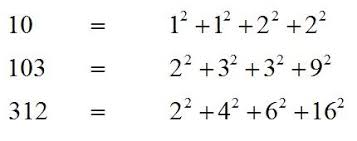
  •     \[\begin{array}{c|c|c|c} a&b&c&x\\ \hline \\2&25&49&38\\2&35&35&36\\5&5&98&54\\5&7&70&41\\5&10&49&32\\5&14&35&27\\7&7&50&32\\7&10&35&26\\7&14&25&23 \end{array}\]

  • De assistente weet uiteraard haar eigen leeftijd en omdat ze het antwoord niet kan geven op de haar gestelde vraag, moet haar leeftijd twee of meer keer voorkomen; dit gebeurt enkel bij (a,b,c,x)=(5,10,49,32)=(7,7,50,32)).
  • Als de leeftijd van de pastoor 51 of meer is, dan blijven bieden mogelijkheden bestaan en zou ze het antwoord dus niet kennen. Als hij jonger is dan 50 voldoen geen van de twee mogelijkheden. Dus is de pastoor 50 jaar en voldoet enkel 5,10 en 49 als leeftijden van de drie parochianen.

Hoogtedriehoek

Geplaatst op door

De hoogtedriehoek van een driehoek ABC is de driehoek gevormd door de  voetpunten van de drie hoogtelijnen van deze driehoek.

Enkele speciale eigenschappen:

  • Het hoogtepunt van driehoek ABC is het middelpunt van de ingeschreven cirkel van zijn hoogtedriehoek.
  • Van alle driehoeken ingeschreven in driehoek ABC(d.i de hoekpunten liggen op de zijden  van driehoek ABC) heeft de hoogtedriehoek de kleinste omtrek.
    Dit wordt ook wel eens het probleem van Fagnano genoemd naar Giovanni Fagnano die dit probleem stelde in 1775.

Toepassingen op stelling van Fermat

Geplaatst op door

Nog even in herinnering brengen, de kleine stelling van Fermat luidt: Als p een priemgetal is Ena en p onderling ondeelbaar zijn dan is

    \[a^{p-1}\equiv 1 \mod p\]

 of

    \[a^p \equiv a \mod p\]

 

Nu een paar toepassingen:

  • n^{13}-n is altijd deelbaar door 2730. Bewijs.
    Spoiler

    • ]We weten dat 2730 = 2.3.5.7.13. Te bewijzen is dan dat n^{13}-n\equiv 0 \mod 2730.
    • Het volstaat dus te bewijzen dat de opgave deelbaar is door de priemfactoren 2,3,5,7,13.
    • En inderdaad n^{13}-n\equiv 0 \mod 2,3,5,7 en 13 met behulp van de stelling van Fermat



  • 5^p-2*3^p+1 is een p-voud als p priem is. Bewijs. 
    Spoiler
    • Modulo p is 5^p\equiv 5 en 3^p÷equiv 3
    • Dus is 5^p-2*3^p+1 \ 5-2*3+1\equiv 0:mod p.




  • 1492^n-1771^n-1863^n+2141^n is steeds deelbaar door 1946. Bewijs dit  en volgende opgaven zelf!
  • n ^2+2n+12 is nooit deelbaar door 112. Tip : vul alle waarden van n in modulo 7.
  • Als n oneven is, dan eindigt de decimale schrijfwijze van 2^{2n}(2^{2n+1}-1) steeds op 28.
  • Voor welke n is n^{n+1}+(n+1)^n een drievoud?

            

Nootje 16

Geplaatst op door

Berekenen alle paren positieve gehele getallen x en y waarvoor

    \[\frac{1}{\log_x 10}+\frac{1}{\log_y 10}\]

een positief geheel getal is met 1<x,y \leq 100.

Antwoord

  • Het is duidelijk dat de oplossingen symmetrisch zijn: als (a,b) een oplossing is dan ook (b,a).
  • Door gebruik van de formule voor verandering grondtal kunnen we de gegeven uitdrukking herleiden tot \log x+\log y=\log(xy).
  • Dus moet \log(xy)=k met k een positief geheel getal; bijgevolg is xy=10^k.
  • Maar 1<xy \leq 10^4, dus is k=1,2,3 of 4.
  • Voor k = 1 vinden we de oplossingen (2,5) en (5,2).
  • Voor k = 2 vinden we (2,50), (50,2), (4,25), (25,4), (5,20), (20,5) en (10,10).
  • Voor k = 3 krijgen we (10,100), (100,10), (20,50),  (50,20), (25,40), (40,25).
  • Voor k = 4 tenslotte vinden we enkel (100,100).