Maandelijks archief: mei 2020

Stelling van Van der Waerden

Geplaatst op door

In de wiskunde zijn er verschillende  stellingen die elk op hun eigen manier zeggen dat totale wanorde onmogelijk is.  Zo hebben we bijvoorbeeld het vermoeden van Baudet: Als je de hele verzameling \mathbb{N} in twee verzamelingen A en B verdeelt, is het dan noodzakelijk zo dat (ten minste) één van die twee verzamelingen willekeurig lange rekenkundige rijtjes bevat?

De Nederlandse wiskundige Van der Waerden publiceerde in 1927 een bewijs. In het artikel staat een algemenere bewering :  voor elk paar positieve gehele getallen r en k is er een getal N zodanig dat indien men {1, 2, …, N }  in r  klassen verdeelt, er minstens een klasse is die een rekenkundige rij van lengte k bevat. Het kleinste getal N waarvoor dit geldt noemt men het Van der Waerden-getal W(r,k).

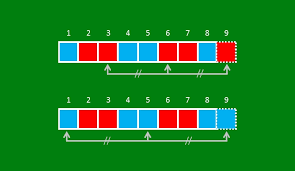
Zo is bijvoorbeeld W(2,3) =  9. Een kleinere waarde is er niet want {{1,2,4,5},{3,4,6,8}} is een verdeling van {1,2,3,4,5,6,7,8} in twee delen die geen rekenkundige rij met 3 elementen bevat. In onderstaande tekening kleur je de getallen van 1 tot en met 9 in 2 kleuren; je ziet dat je steeds een rekenkundige rij van drie elementen krijgt in eenzelfde kleur.

Kansen en matrices

Geplaatst op door

Een cavia bevindt zich in kamer 2. Ze kan deze kamer verlaten naar kamer 3,1 of 5 en dit met even grote waarschijnlijkheid. Hoe groot is de kans dat de cavia zich na 4 verplaatsingen in kamer 5 bevindt?

Noteer met a,b,c,d,e de kans dat de cavia zich op een zeker moment   in kamer 1,2,3,4,5 bevindt. Met a_i,b_i,c_i,d_i,e_i noteren we de kans dat het beestje zich, na i verplaatsingen, in kamer 1,2,3,4,5 bevindt. 

Dan is bijvoorbeeld a_1=0*a+\frac{1}{3}*b+\frac{1}{3}*c+\frac{1}{3}*d+\frac{1}{3}*e. We kunnen voor b_1,c_1,d_1,e_1 gelijkaardige formules vinden. Het is makkelijker die gegevens in een matrix M te steken die de overgang regelt van a,b,c,d,e naar a_1,b_1,c_1,d_1,e_1. De overgang wordt geregeld door A_1=M*A, hierbij is A=(a,b,c,d,e)^t ,A_1=(a_1,b_1,c_1,d_1,e_1)^t en 

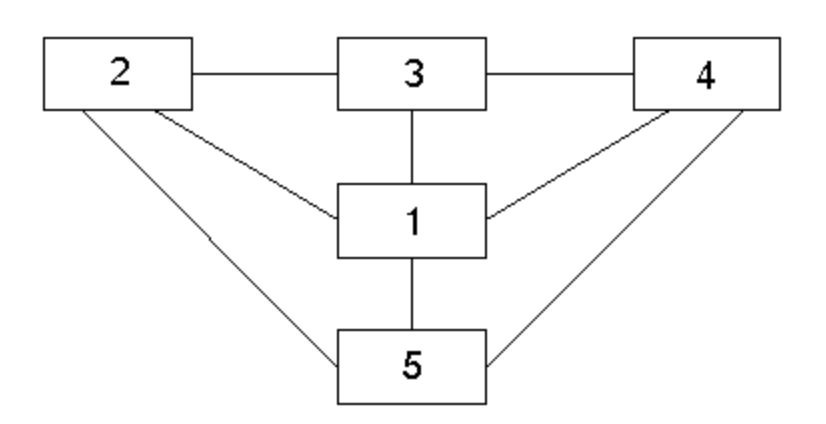
    \[M= \begin{pmatrix}0&\frac{1}{3}&\frac{1}{3}&\frac{1}{3}&\frac{1}{3}\\\frac{1}{4}&0&\frac{1}{3}&0&\frac{1}{3}\\\frac{1}{4}&\frac{1}{3}&0&\frac{1}{3}&0\\\frac{1}{4}&0&\frac{1}{3}&0&\frac{1}{3}\\\frac{1}{4}&\frac{1}{3}&0&\frac{1}{3}&0\end{pmatrix}\]

Het is duidelijk dat bij de vierde verplaatsing A_4=M^4*A.

Berekening met een rekentoestel geeft:

    \[A_4=\begin{pmatrix}0,20987654\\0,21219136\\0,11342593\\0,21219136\\0,05555556\end{pmatrix}\]

Er is dus ongeveer 5,56% kans dat de cavia zich na 4 verplaatsingen in kamer 5 zit.

Derangement

Geplaatst op door

Een derangement is een permutatie zonder vaste punten, met andere woorden een ordening waar geen enkel element op de juiste plaats staat.  Het aantal derangements van n verschillende elementen wordt aangeduid met !n : subfaculteit. Het probleem van het tellen van het aantal derangementen werd in 1708 voor het eerst beschouwd door Pierre Raymond de Montmort, die het probleem oploste in 1713, ongeveeer tegelijkertijd met Nicolaas Bernoulli.

Voor 3 elementen zijn er 3! = 6 permutaties. De ordeningen  312 en 231 zijn derangements. Het zijn de enige, dus !3=2. Voor 4 elementen is, het al wat moeilijker:

Hierboven zie je de 24 permutaties van de 4 elementen {1,2,3,4}. De blauwe zijn de derangements, dus !4=9. Je kan nagaan dat !5=44, !6= 265 en !7=1854. Er zijn echter ook formules beschikbaar om de subfaculteiten uit te rekenen:

    \[\text{!n}=(n-1)[!(n-1)+!(n-2)]\]

    \[\text{!n}=n!\sum_{i=0}^n\dfrac{(-1)^i}{i!}\]

 

Uit deze laatste formule kan je de verhouding tussen !n en n! afleiden:

    \[\dfrac{!n}{n!}=\dfrac{1}{e} \approx 0,368\]

Het 3n+1 vermoeden

Geplaatst op door

Neem een natuurlijk getal n. Als het even is, deel het door 2. Als het oneven is, vermenigvuldig je het met 3 en tel er 1 bij op. Met de uitkomst doe je hetzelfde, en dat blijf je maar herhalen.

Neem bijvoorbeeld 6, dan ontstaat volgende rij : 6,3,10,5,16,8,4,2,1. We noemen dit de Collatz rij van 6. De lengte van deze Collatz rij is 9. De lengte van dergelijke rij kan snel oplopen. Zo is de lengte van de  Collatz rij van 27 gelijk aan 111.

Het 3n + 1-vermoeden zegt dat bovengenoemd iteratieproces bij iedere mogelijke startwaarde altijd een keer bij 1 zal uitkomen. De precieze oorsprong van het 3n + 1- vermoeden is niet helemaal duidelijk. In de jaren dertig was Lothar Collatz( 1910-1990), een Duitse wiskundige, met soortgelijke problemen bezig, en het 3n + 1-probleem wordt algemeen aan hem toegeschreven. Het is tot op heden nog steeds niet bewezen.

Er zijn enkele aanwijzingen dat het vermoeden van Collatz juist is. Voor alle getallen onder 10^{19}   is inmiddels gecontroleerd dat ze aan het vermoeden voldoen. Het probleem met het controleren is dat het alleen het vermoeden kan weerleggen. Als het vermoeden waar is, kan er geen bewijs voor gevonden worden op deze manier.

Bewijzen met verhaaltjes

Geplaatst op door

Hoe bewijs je volgende formule? 

    \[k(k-1)\binom{n}{k}=n(n-1)\binom{n-2}{k-2}\]

Het gaat zeer snel door gebruik te maken van de definitie van  binomiaalcoëfficiënten. Maar er is ook een andere manier, die je ook kan gebruiken als het gebruik van de definitie wat ingewikkelder ligt. We verzinnen gewoon een verhaaltje …

Je wilt op school met n leerlingen een leerlingenraad van k personen oprichten, waarbij een voorzitter en een ondervoorzitter moeten aangeduid worden.

  • Het linkerlid van bovenstaande vergelijking komt overeen met volgende procedure: kies eerst k leden uit de n leerlingen. Dit  kan op \binom{n}{k} manieren. Kies in die groep van k gekozenen een voorzitter ( k mogelijkheden) en een ondervoorzitter ( k-1 mogelijkheden).
  • Het rechterlid correspondeert met de procedure: kies uit de n leerlingen eerst een voorzitter ( n mogelijkheden), dan een ondervoorzitter( n-1 mogelijkheden) en vul tenslotte aan tot je een groep van k leden hebt. Je moet dus nog k-2 leerlingen kiezen uit de n-2 beschikbare (\binom{n-2}{k-2} mogelijkheden).
  • Aangezien beide procedures hetzelfde probleem oplossen , zijn linkerlid en rechterlid gelijk aan elkaar.