Maandelijks archief: april 2020

Magische driehoek

Geplaatst op door

Plaats de cijfers van 1 tot en met 9 in de cirkeltjes in het diagram zodat de som van de vier cijfers langs de drie zijden gelijk is aan 17. En hoe kan je ze rangschikken zodat de som langs de drie zijden telkens gelijk is aan 20? Is er een andere som mogelijk? 

Deze puzzel komt uit het boek The Moscow puzzels van Boris Kordemsky(1907-1999), een wiskundedocent uit Moskou.

Spoiler

  • Noteer de som langs de drie zijden door x en de som van de elementen in de hoekpunten door s.
  • de som van alle cijfers 1 tot 9 is 45.
  • Dus 45=3x – s. Hieruit volgt dat s een drievoud moet zijn.
  • Voor x = 17 vinden we s = 6 en krijgen we volgende oplossing:
  • voor x = 20 vinden we s= 15 en vinden we de oplossingen:
  • We vinden ook een oplossing voor x = 21 met s = 18:
  • Andere oplossingen hebben we niet gevonden.

Veelhoeksgetallen

Geplaatst op door

Dit artikel is van de hand van Hannah Prause, leerlinge van 6MTWI van het H.Drievuldigheidscollege in Leuven.

Veelhoeksgetallen zijn voorbeelden van figuratieve getallen: getallen die kunnen gevormd worden door figuurtjes te maken met bijvoorbeeld rijstkorrels of steentjes. Een veelhoeksgetal is dus een getal dat het aantal stippen is van een figuur met een in een hoekpunt geneste regelmatige veelhoek. Vanuit een hoekpunt (een buitenste stip) vertrekt dus steeds een regelmatige veelhoek.

De meest gekende zijn de driehoeksgetallen en de vierkantsgetallen of kwadraten.

 

Hierboven zie je hoe je het n-de driehoeksgetal T_n kan vinden: Het is duidelijk dat

    \[T_n=1+2+\cdots+n=\dfrac{n(n+1)}{2}\]

De kwadraatgetallen zijn uiteraard 1,4,9,16,… Interessant is dat sommige getallen zowel driehoeksgetallen als kwadraten zijn. Het eerste dergelijk getal is uiteraard 1. Pas bij 36 vinden we nog een getal dat in punten zowel een driehoek als een vierkant kan vormen; daarna komt 1225 en 41616.

Er bestaat een algemene formule om het n-de k-hoeksgetal te bepalen:

    \[T_k(n)=(0,5k-1)n^2-(0,5k-2)n\]

In tegenstelling tot een veelhoeksgetal gedefinieerd vanuit een hoekpunt ( zoals hierboven besproken) bestaat een gecentreerd veelhoeksgetal uit steeds groter wordende veelhoeken rond een centraal punt. hieronder zie je links een voorbeeld van een vijfhoeksgetal en rechts een voorbeeld van een gecentreerd vijfhoeksgetal

Gecentreerde veelhoeksgetallen hebben geen gemeenschappelijk hoekpunt en worden beschreven volgens volgende formule: 

    \[C_k(n)=0,5k*n^2-0,5k*n+1\]

Hierboven zie je het vierde vijfhoeksgetal en het vierde gecentreerd vijfhoeksgetal: T_5(4)=22 en C_5(4)=31

Derde afgeleide

Geplaatst op door

De afgeleide of het differentiaal quotiënt is een maat voor verandering van een functie ten opzichte van verandering van zijn variabelen. Als de afgeleide van een functie f gedefinieerd is voor alle punten in het domein van f, wordt de daardoor bepaalde functie de afgeleide functie of kortweg de afgeleide genoemd. Het concept van de afgeleide van een functie werd in de 17e eeuw vrijwel tegelijkertijd door Isaac Newton en Gottfried Leibniz uitgevonden.

In Coronatijden wordt wel elke dag iets over de afgeleide verteld: het aantal besmettingen ( N(t)) stijgt, betekent dat de eerste afgeleide N'(t) groter is dan 0. De stijging van het aantal besmettingen neemt af, de kromme vlakt af, betekent dat de tweede afgeleide N”(t) negatief is.

De vraag die Leander Saerens, leerling van 6WEWI uit het H.Drievuldigheidscollege in Leuven, zich stelde was: heeft de derde afgeleide van een functie ook een ‘interessante’ betekenis.

Voor willekeurige functies ligt dat wat moeilijk, maar er is wel een betekenis te geven als we naar de fysische toepassingen kijken. In de natuurkunde  spelen afgeleiden ook een zeer belangrijke rol. Zo bepaalt de eerste afgeleide van de plaats functie de snelheid en bepaalt de tweede afgeleide van de plaats functie (of de eerste afgeleide van de snelheidsfunctie) de versnellingsfunctie.

De derde afgeleide, of de verandering van de versnelling, wordt  ‘jerk’ genoemd, van het werkwoord ‘to jerk’, rukken. Zo kan je bijvoorbeeld denken aan de plotselinge ruk aan een touw. in een auto kan je het effect van een kerk of ruk goed voelen. een ervaren chauffeur zal zachtjes versnellen. Een beginnende rijder zal meer met horten en stoten rijden, zeker bij het veranderen van versnelling.

 

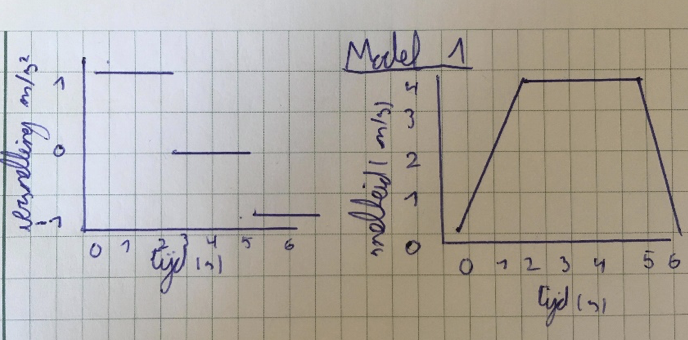
Een voorbeeld met een lift: 

in een eerste model gaat men uit van een constante versnelling  bij het versnellen en  bij het vertragen. Tussenin blijft de lift met zijn maximale snelheid bewegen.

            

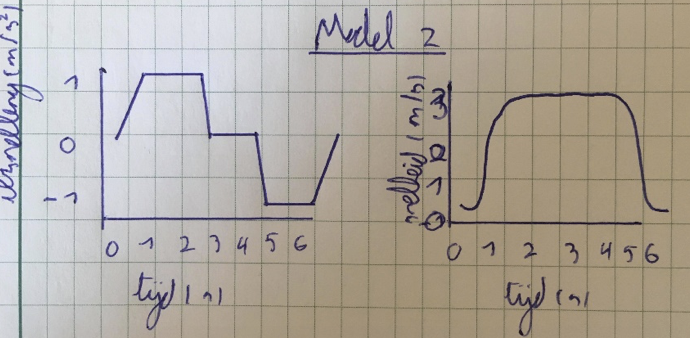
in een tweede model stijgt de versnelling lineair stijgt tot haar maximale waarde, ze blijft op haar maximale waarde, en neemt daarna lineair af .Dan is de snelheid maximaal en dit blijft zo gedurende enige tijd. Daarna vindt eenzelfde soort proces plaats maar dan omgekeerd om de snelheid weer tot 0 m/s te brengen. 

In differentiaalmeetkunde wordt de derde afgeleide onder andere ook gebruikt om de torsie van een ruimtekromme te berekenen. De torsie van een ruimtekromme zegt hoe sterk deze kromme afwijkt van een vlak. De torsie wordt uitgedrukt in radialen/lengte-eenheid en kan positief, nul of negatief zijn. Indien een ruimtekromme in een vlak ligt is haar torsie nul. 

Stelling van Pythagoras

Geplaatst op door

Deze tekst is gemaakt door Joran Deschagt, leerling van 6WEWI uit het H.Drievuldigheidscollege in Leuven.

 

    \[a^2+b^2=c^2\]

Iedereen kent de stelling dat in een rechthoekige driehoek de som van de kwadraten van de rechthoekszijden gelijk is aan het kwadraat van de schuine zijde. Wij kennen deze stelling als de stelling van Pythagoras. Maar deze stelling was al gekend bij de Soemeriërs en de Egyptenaren, lang voor Pythagoras.

Er zijn in feite heel  veel verschillende bewijzen voor de stelling van Pythagoras. Ook werden deze over heel de wereld ontworpen, van Azië tot Amerika. Er was er zelfs één van de Amerikaanse president, J. A. Garfield. We geven een kleine selectie:

Het oudste bewijs dat we hebben gevonden situeren we ergens tussen 1200 v.C. – 100v.C. in een oud Chinese leerboek Chou-Pei Suan Ching.

De zijde van het grote vierkant is a + b en de oppervlakte dus (a+b)^2. Hierbij zijn a en b de zijden van de rechthoekige driehoeken die getekend staan tussen het grote vierkant en het kleine vierkant. De zijde van het middelste vierkant is c. De oppervlakte van het grote vierkant is de som  van  de oppervlakten van de 4 rechthoeken en de oppervlakte van het kleine vierkant: (a+b)^2=4. \frac{ab}{2}+c^2. Hieruit volgt dan de stelling van Pythagoras.

Het bewijs van president Garfield steunt op de oppervlakte van een trapezium

De oppervlakte van het trapezium is gelijk aan de som van de oppervlakten van de drie driehoeken, dus (a+b).\frac{a+b}{2}=\frac{ab}{2}+\frac{ab}{2}+\frac{c^2}{2}. Uitrekenen geeft ….de stelling van Pythagoras!

 

Een recenter bewijs komt van Xiaolin Zhong, professor aan het UCLA:

Draai de driehoeken ABH en BCD naar de driehoeken HGF en FED; Je ziet hier 4 keer die driehoek ‘rond’ het binnenste vierkant en 2 keer in dat binnenste vierkant. Het grootste vierkant heeft  een zijde van a + b en een oppervlakte gelijk aan (a+b)^2 en bestaat uit 4 rechthoeken en een vierkant met zijde EG. Het vierkant FDCH heeft oppervlakte c^2 en bestaat uit 4 driehoeken (die 2 rechthoeken vormen) en dat vierkant met zijde EG. Hieruit kan je het gewenste resultaat afleiden.

 

Wat is algebra?

Geplaatst op door

Het woord ‘algebra’ komt uit een werk van Al-Khwarizimi dat Hisab Al-Jabr w’Al-Muqabala heet en waarbij Al-Jabr algebra werd.

Als we het over algebra hebben, dan bedoelen we hier de algebra die op de middelbare scholen wordt gegeven: de algebra die rekenkundige bewerkingen uitvoert op getallen en variabelen, oftewel dingen die er uit zien als 5x^2+x=2.

De algebra is echter niet in die vorm ontstaan.

  • De eerste ontwikkelingsfase was de retorische algebra. Men maakt gebruik van volledige zinnen. Dit deed men tot de derde eeuw. 5x^2+x=22 zou dan worden gegeven als  vijf keer het vierkant van een hoeveelheid ,vermeerderd met de hoeveelheid is 22. De retorische notaties ontwikkelden zich rond 2000 v. chr.
  • Een tweede fase was de gesyncopeerde algebra (beschrijvingen vermengd met afkortingen en wiskundige symbolen) zoals in de werken van Diophantus en Brahmagupta. Dit was al een verbetering maar het vergde toch nog veel extra werk in vergelijking wat later kwam. Deze fase ontwikkelde zich rond 250 na chr.
  • De laatste fase is de symbolische algebra. Deze kwam tot stand rond 1600 en kwam vooral tot bloei in het werk van Descartes.

Daarnaast doorliep de algebra ook verschillende soorten van abstractie:

  • Meetkundig stadium  waar de begrippen van algebra zijn grotendeels geometrische . Dit dateert uit de  tijd van de Babyloniërs en werd voortgezet met de Grieken.
  • Statische fase , waarbij het doel is om getallen te vinden  die aan bepaalde relaties voldoen. 
  • Dynamische stadium , waarin  beweging de achterliggende gedachte was: het idee van een functie 
  • Abstract stadium , waar de wiskundige structuur speelt een centrale rol. Abstract algebra is grotendeels een product van de 19e en 20e eeuw.