Maandelijks archief: december 2019

Catalan veelvlakken

Geplaatst op door

Een Catalan veelvlak is de duale figuur van een Archimedisch veelvlak.  Ze werden vernoemd naar de Belgische wiskundige Eugène Catalan( 1814-1894). Twee figuren heten duaal als de middelpunten van de zijvlakken van de ene figuur ,de hoekpunten van het andere veelvlak vormen, en omgekeerd.

Enkele eigenschappen:

  • De Catalan veelvlakken zijn convex.
  • Ze zijn zijvlak transitief, m.a.w. alle zijvlakken zijn bijvoorbeeld driehoeken. Ze hoeven niet gelijkzijdig te zijn.

 

Een mooi voorbeeld is te zien op het Atomium ( ontwerp van A.Waterkeyn en de broers Polak): de disdyakis dodecahedron, een veelvlak met 48 zijvlakken die allemaal driehoeken zijn

Halfregelmatige veelvlakken

Geplaatst op door

 

Half regelmatige veelvlakken zijn veelvlakken die voldoen aan volgende eigenschappen:

  • Alle zijvlakken zijn regelmatige veelhoeken.
  • Hoekpunt transitief: in ieder hoekpunt komen steeds dezelfde veelhoeken samen in dezelfde of tegengestelde volgorde.

We onderscheiden 3 soorten:

  1. Een oneindige reeks prisma’s ( 2 regelmatige n-hoeken verbinden met n vierkanten)
  2. Een oneindige reeks anti-prisma’s (2 regelmatige n-hoeken over 180°/n draaien en dan verbinden met 2n gelijkzijdige driehoeken)
  3. Dertien Archimedische lichamen

 

 

Eenheden in ZC_n

Geplaatst op door

In dit artikel beschrijven we hoe we eenhedengroepen van \mathbb{Z}C_n berekenen. We verdelen het werk in 3 delen: n priem, n een priem macht en n geen priem macht. In elk van de gevallen rekenen we twee voorbeelden volledig uit, dikwijls op verschillende manieren. Met de beschreven technieken hopen we , voor elke waarde van n, de eenheden groepen te kunnen beschrijven.

Regelmatige veelvlakken

Geplaatst op door

Een regelmatig veelvlak is een veelvlak met volgende eigenschappen:

  • Alle zijvlakken zijn congruente regelmatige veelhoeken.
  • In elk hoekpunt komen evenveel zijvlakken samen.
  • Ze zijn convex
  • De hoeken tussen de zijvlakken zijn steeds hetzelfde.
  • Voor het aantal ribben (R), het aantal grensvlakken (G) en aantal hoekpunten (H) van een convex lichaam geldt de formule van Euler: R + 2 = G + H

Er zijn er 5; ze worden ook wel eens de Platonische lichamen genoemd naar Plato(427 BC – 347BC), die ze het eerst beschreef.

Plato bracht de vijf regelmatige veelvlakken ook in verband met de vijf kosmische bouwstenen van de wereld: vuur, lucht, water, aarde en hemelmaterie.

Verbindt men de middens van de zijvlakken van een veelvlak met elkaar, dan vormen de verbindingslijnen de ribben van een ander veelvlak. Een viervlak blijft een viervlak, maar een kubus wordt een octaëder en omgekeerd. Een dodecaëder wordt een icosaëder en omgekeerd. De kubus en de octaëder zijn het duale veelvlak van elkaar, de dodecaëder en de icosaëder ook.

De huwelijksstelling van Hall

Geplaatst op door

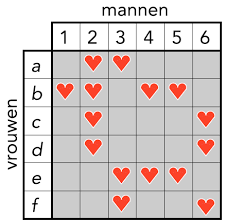
Zes vrouwen vallen elk op een aantal vrijgezelle mannen. Kunnen de zes vrouwen met de zes mannen worden gekoppeld, zó dat elke vrouw een man van haar keuze trouwt?

In sommige gevallen is het eenvoudig om te zien dat er geen oplossing mogelijk is. Als er een dame bij is die niemand leuk vindt, lukt het niet. Ook als er twee vrouwen zijn die enkel één en dezelfde man willen, loopt het mis.

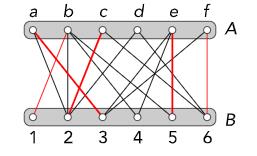
Kan het met de volgende keuze?
Een nodige en voldoende voorwaarde op het bestaan van een oplossing is dat iedere k dames samen met tenminste k  verschillende mannen willen trouwen. Hierbij is 1 \leq k\leq6. Omdat de dames a,c,d en f samen maar drie verschillende mannen willen huwen, namelijk de nummers 2,3 en 6, is het dus onmogelijk alle zes dames uit te huwelijken!

Deze stelling, die dateert uit 1933, werd bewezen door de Engelse wiskundige Philip Hall ( 1904-1982).

Als het zo is dat we niet alle dames kunnen koppelen, dan kunnen we ons wel de vraag stellen: wat is het maximaal aantal dames dat kan gekoppeld worden?

Hiervoor vertalen we het probleem naar een probleem met grafen: Voor iedere vrouw is er een bijhorend punt in A en voor iedere man is er een punt in B. We trekken een lijn tussen een vrouw en een man, als zij met hem wilt trouwen.

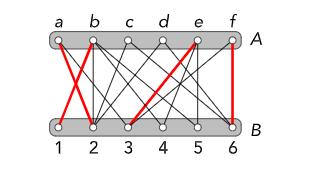
De resulterende graaf heet bipartiet omdat de punten zijn opgedeeld in twee groepjes en lijnen altijd punten uit verschillende groepen verbinden. Een aantal lijnen noemt men een matching als geen twee lijnen eenzelfde eindpunt hebben. Een uithuwelijking is dus eigenlijk een matching. In het rood staat hierboven een matching met 4 lijnen. Een betere matching wordt gegeven door volgende figuur, waarin 5 vrouwen kunnen worden uitgehuwelijkt.