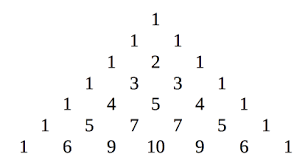Maandelijks archief: augustus 2019

Uitdaging 3 en 4

Geplaatst op door

Voor welke waarden van k is x^3+y^3+z^3+kxyz deelbaar door x+y+z?

Antwoord

  • Als x^3+y^3+z^3+kxys deelbaar is door x+y+z, dan bestaat er een Q(x,y,z) zodat

        \[x^3+y^3+z^3+kxyz=(x+y+z)Q(x,y,z)\]

  • Vervang nu in beide leden x door 2, en y en z door -1, dan vind je 8-1-1+2k=0 of m.a.w. k=-3.

Een veelterm f(x)  met gehele coëfficiënten heeft oneven getalwaarden voor 0 en 1. Bewijs dat  f(x) geen gehele nulwaarden kan hebben.

Antwoord

  • Noteer de veelterm f(x)=a_nx^n+\cdots+a_1x+a_0.
  • Omdat f(0) oneven is moet a_0 een oneven getal zijn.
  • Omdat f(1) even is moet a_n+\cdots+a_1+a_0 ook oneven zijn.
  • Stel nu dat c een gehele nulwaarde is van f(x), dan is a_nc^n+\cdots+a_1c+a_0=0.
  • Als c even is dan is het linkerlid van deze ongelijkheid oneven en kan dus nooit nul zijn.
  • Als c oneven is, dan krijgen we modulo 2 dat a_n+\cdots+a_1+a_0 \equiv 0. Maar ook dat is onmogelijk want het linkerlid is oneven en kan dus nooit  nul zijn.
  • Dus heeft f(x) geen gehele nulwaarden.

De Rascal driehoek

Geplaatst op door

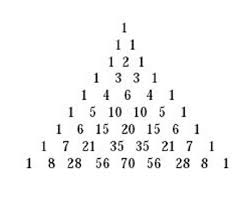
Als men, bij een IQ-test, zou vragen  om de driehoek te voltooien, dan krijg je meestal als antwoord:

Dit is de driehoek van Pascal. Vervolledigen kan via de formule

    \[u_{n,r}=u_{n-1,r-1}+u_{n,r-1}\]

Hierbij geeft r de rij weer en n de plaats op de rij. Zowel r als n starten bij de waarde 0.

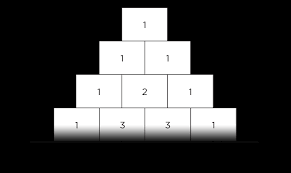
Maar dit is niet het enige patroon dat je kan gebruiken. Wat denk je van volgend antwoord:

Het waren 3 middelbare school leerlingen,  Alif Anggoro, Eddy Liu, Angus Tulloch  uit de USA, Canada en Indonesië die dit verband beschreven met de formule

    \[u_{n,r}=n(r-n)+1\]

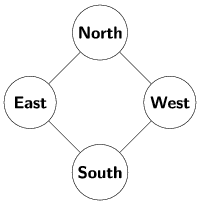
Je kan ook gebruik maken van de diagonaalformule :

Het getal op zuid is ( oost x west +1 ) : noord. Bij de driehoek van Pascal was zuid = oost + west.

Eigenaardig genoeg is elk element in de Rascal driehoek een natuurlijk getal! Net zoals bij de driehoek van Pascal kan je ook hier een paar mooie patronen terugvinden. Kijk maar naar de diagonalen van de Rascal driehoek