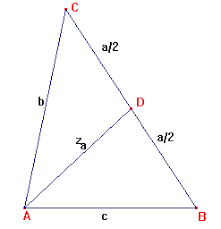
Om de lengte van een zwaartelijn te berekenen, gebruiken we de cosinusregel in de driehoeken ABD en ACD voor ![]() en
en ![]() . Optellen van de formules geeft:
. Optellen van de formules geeft:
![]()
Als ![]() dan is
dan is ![]() . Want
. Want ![]() . Dus bij de langste zijde hoort de kortste zwaartelijn.
. Dus bij de langste zijde hoort de kortste zwaartelijn.
Het berekenen van de lengte van een bissectrice is heel wat lastiger. Noteer ![]() en
en ![]() .
.
Een bissectrice in een driehoek verdeelt de overstaande zijde in de verhouding van de aanliggende zijdes, dus ![]() . Volgens de eigenschappen van evenredigheden volgt hieruit dat
. Volgens de eigenschappen van evenredigheden volgt hieruit dat ![]() of
of ![]() en analoog
en analoog ![]() . Teken nu een punt E zodat de hoek ACE gelijk is aan de hoek ADB. Uit de gelijkvormigheid van de driehoeken ACE en ADB volgt dat
. Teken nu een punt E zodat de hoek ACE gelijk is aan de hoek ADB. Uit de gelijkvormigheid van de driehoeken ACE en ADB volgt dat ![]() en uit de gelijkvormigheid van de driehoeken DEC en ABD volgt dat
en uit de gelijkvormigheid van de driehoeken DEC en ABD volgt dat ![]() . Door die twee formules van elkaar af te trekken vinden we dat:
. Door die twee formules van elkaar af te trekken vinden we dat:
![]()
Net zoals bij de zwaartelijnen kunnen we besluiten dat bij de langste zijde de kortste bissectrice hoort.
Door gebruik te maken van deze formules kan je door algebraïsche berekeningen meetkundige eigenschappen bewijzen, zoals bijvoorbeeld: De langste bissectrice is minstens even lang als de kortste zwaartelijn. Als ![]() dan komt dit neer op
dan komt dit neer op ![]() .
.