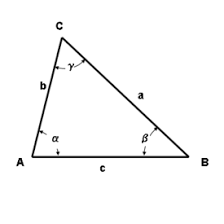
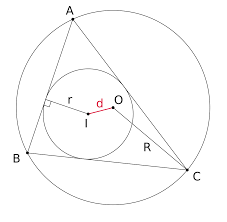
We geven 7 eigenschappen die, bij het onderzoeken van eigenschappen van een driehoek, zeer nuttig kunnen zijn. Noteer de halve omtrek van de driehoek met s en de oppervlakte met K. Verder zijn r en R respectievelijk de stralen van de ingeschreven en omgeschreven cirkel.
 .
. . (formule van Heroon)
. (formule van Heroon)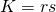 .
. .(sinusregel)
.(sinusregel)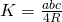 .
. .
.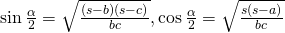 .
.