Maandelijks archief: juli 2018
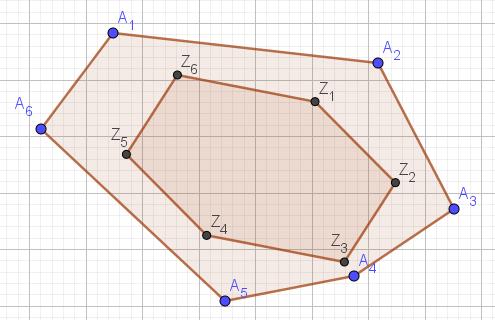
Een nieuwe zeshoek
Neem een willekeurige convexe zeshoek. Met telkens drie opeenvolgende hoekpunten van deze zeshoek vormt men zes driehoeken. Construeer het zwaartepunt van deze driehoeken. De alzo verkregen punten zijn de hoekpunten van een nieuwe zeshoek. Toon aan dat de paren overstaande zijden van deze zeshoek evenwijdig en even lang zijn.
We geven de hoekpunten ![]() van de oorspronkelijke zeshoek willekeurige coördinaten
van de oorspronkelijke zeshoek willekeurige coördinaten ![]() ( drievouden omdat we het zwaartepunt moeten berekenen). Het zwaartepunt van driehoek
( drievouden omdat we het zwaartepunt moeten berekenen). Het zwaartepunt van driehoek ![]() is het punt
is het punt ![]() . Analoge coördinaten voor de andere hoekpunten. We proberen nu aan te tonen dat
. Analoge coördinaten voor de andere hoekpunten. We proberen nu aan te tonen dat ![]() evenwijdig is met
evenwijdig is met ![]() en dat
en dat ![]() .
.
- De richtingsgetallen van
 zijn
zijn 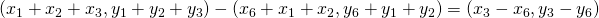 De richtingsgetallen van
De richtingsgetallen van  zijn
zijn  Bijgevolg is
Bijgevolg is  evenwijdig met
evenwijdig met  .
.  .
.
Tournament of the towns
De wedstrijd Tournament of Towns (TT) onderscheidt zich van vele andere vergelijkbare competities door haar filosofie die veel meer berust op vindingrijkheid dan puur op kennis of vaardigheden. Ten eerste zijn problemen moeilijk (vooral in A-niveau in de Senior-divisie waar ze vergelijkbaar zijn met die op de International Mathematical Olympiad, maar veel ingenieuzer en minder technisch). Ten tweede kunnen de deelnemers zelf de problemen kiezen die ze leuk vinden, want de score van de deelnemer is de som van zijn 3 beste antwoorden. De problemen zijn meestal combinatorisch, met af en toe een beetje meetkunde, getaltheorie of algebra. Elk jaar zijn er twee rondes: de lente en de herfst compettitie
De TT is van oorsprong een Russisiche wiskunde-wedstrijd . Ze is opgestart door wiskundige Nikolay Konstantinov. De eerste wedstrijd, gehouden in het academisch jaar 1979-1980, werd de Olympiad of Three Towns genoemd. Die steden waren Moskou, Kiev en Riga. De reputatie van de competitie groeide en het volgende jaar heette het Tournament of the Towns. Momenteel nemen studenten deel uit meer dan 100 steden in landen over de hele wereld, waaronder Australië, Oostenrijk, Bulgarije, Canada, Columbia, Duitsland, Groot-Brittannië, Israël, Rusland, Slovenië, Oekraïne en de Verenigde Staten.
Meer info met onder andere de archieven vind je op volgende website.
Eenvoudige ongelijkheden
Het is voor iedereen duidelijk dat een kwadraat van een reeël getal nooit negatief kan zijn. Het uitwerken van ![]() geeft ons twee eenvoudige ongelijkheden, waarmee we snel aan het werk kunnen ( veronderstel alle getallen positief):
geeft ons twee eenvoudige ongelijkheden, waarmee we snel aan het werk kunnen ( veronderstel alle getallen positief):
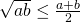 .
. .
.
Twee voorbeelden:
- Bewijs dat
 .
.
Uit formule 1 vinden we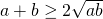 , maar ook dat
, maar ook dat  en
en  , dus is
, dus is  .
. - Bewijs, als
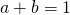 , dan is
, dan is  .
.
Uit formule 2 volgt het linkerlid groter is dan of gelijk is aan . Uit formule 1 weten we dat
. Uit formule 1 weten we dat 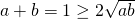 ofwel
ofwel  . Hieruit volgt dat
. Hieruit volgt dat 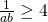 .
.
Bijgevolg is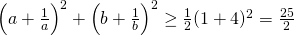 .
.
Waar komt de naam ‘wiskunde’ vandaan?
Het Nederlands woord wiskunde stamt uit de 17 de eeuw en komt van Simon Stevin (1548-1620) die het woord wisconst gebruikte. Het ‘wis’ in het woord betekent zeker weten ( kijk naar de uitdrukking: wis en waarachtig ). Wiskunde is dus de kunde of vaardigheid van het zeker weten en dit doen we door elke uitspraak te bewijzen.
In de meeste andere talen wordt bijna steeds hetzelfde woord voor wiskunde gebruikt: mathematics, mathematica, mathematique, Mathematic,… allemaal afgeleid van het Griekse woord ‘mathein’ dat ‘leren’ betekent.
Aristoteles had het menselijk kunnen verdeeld in 2 delen: mechanische of handwerkkunsten (de latere ambachten), en de vrije kunsten de latere wetenschappen). Kunste in deze context betekende : kunde, vaardigheid. Tot de eerste groep behoorde alles wat met vaardigheden te maken had, of het nu het werk van de timmerman betrof of dat van de kunstschilder. De vrije kunsten daarentegen waren die vakken waarvoor men hersenwerk nodig had. Ze werden de ‘vrije kunsten’ genoemd omdat zij enkel konden worden uitgeoefend door hen die vrij waren gesteld van lichamelijke arbeid en materiële zorgen. De 7 vrije kunsten waren 7 vakken die deel uitmaakten van het studieprogramma in de antieke en de Middeleeuwse universiteiten.
De 7 vrije kunsten werden dan weer onderverdeeld in enerzijds het trivium , de taalvakken: retorica, grammatica en dialectica. Ze zijn te begrijpen zonder verdere studie ( vandaar het woord ’triviaal’ ). Anderzijds was er ook het quadrivium , met de rekenvakken arithmetica (rekenkunde), geometria (meetkunde), musica (harmonieleer) en astronomia (kosmologie), die moeten geleerd worden.
We zien hier ook twee fundamentele aspecten van de wiskunde opduiken: getal – ruimte
- rekenkunde en harmonieleer representeren het getal, de hoeveelheid.
- meetkunde en kosmologie vertegenwoordigen de vorm, de hoedanigheid.