In deze tekst bestuderen we eenheden groepen in orders van getallenvelden en eenheden groepen in niet-commutatieve orders.
Maandelijks archief: juni 2018
De rechte van Wallace
Er bestaat een mooie, minder bekende meetkundige stelling, die voor het eerst gevonden werd door de Schotse wiskundige William Wallace (1768-1843).
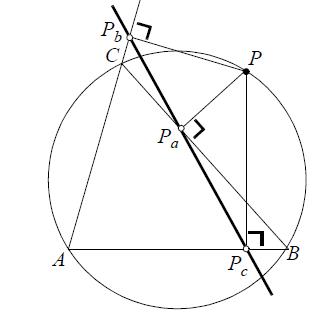
De voetpunten Pc , Pa en Pb van de loodlijnen uit een punt
P van de omgeschreven cirkel van driehoek ABC neergelaten
op de dragers van de zijden, zijn collineair.
De rechte door Pa,Pb en Pc noemt men de rechte van Wallace.
Het bewijs verloopt als volgt: PBPcPa is een koordenvierhoek (hoek tussen zijde en diagonaal). Analoog zijn ook PPaCPb en PCAB koordenvierhoeken. Omdat de overstaande hoeken supplementair zijn volgt hieruit dat 
. Hieruit volgt dat de drie punten collineair zijn.
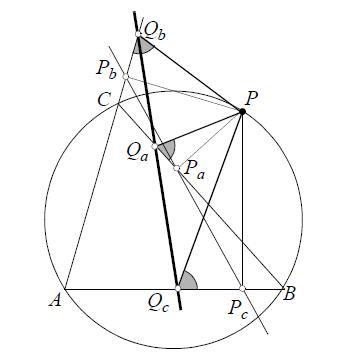
Men kan deze stelling ook veralgemenen:
Als je in plaats van loodlijnen, rechten uit P kiest die eenzelfde hoek maken met de zijden, dan geldt weer dat de drie ‘voetpunten’, zeg Qc, Qa en Qb, collineair zijn.
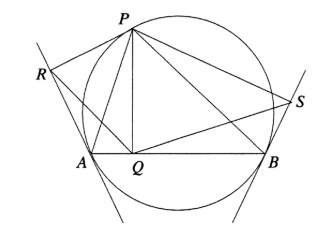
Opgave 20
AB is een koorde en P een willekeurig punt van een gegeven cirkel. Q is de loodrechte projectie van P op AB en R en S zijn de loodrechte projecties van P op de raaklijnen aan de cirkel in A en B. Bewijs dat PQ het meetkundig gemiddelde is van PR en PS.
Antwoord
- Maken we eerst een tekening:
- We proberen aan te tonen dat de driehoeken PRQ en PQS gelijkvormig zijn, want dan is
en hieruit volgt het gestelde. - De vierhoeken PRAQ en PQSB zijn koordenvierhoeken omdat twee overstaande hoeken recht zijn.
- In de eerste koordenvierhoek is
omdat in een koordenvierhoek de hoek tussen een zijde en de diagonaal gelijk is aan de hoek gevormd door de overstaande zijde en de andere diagonaal. Daarom is ook 
. - Maar de hoeken
en 
zijn gelijk als hoeken op eenzelfde boog in de gegeven cirkel. Bijgevolg is 
. - Via een analoge redenering is ook
en dus zijn de driehoeken PRQ en PQS gelijkvormig, zoals gevraagd.
Enkelvoudige groepen
De classificatie stelling van eindige enkelvoudige groepen classificeert alle eindige enkelvoudige groepen. Deze groepen zijn de bouwstenen van alle eindige groepen, zoals de priemgetallen de bouwstenen zijn van de natuurlijke getallen. De stelling beslaat meer dan 10000 pagina’s verspreid over meer dan 500 artikels in de periode van 1955 tot 1983. Michael Aschbacher en Steve Smith hebben de laatste puntjes op de spreekwoordelijke i geplaatst.
De enkelvoudige groepen zijn:
- de cyclische groepen
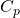van priem orde. - de alternerende groepen
met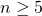 
. - de Chevalley groepen en de gedraaide Chevalley groepen.
- De Tits groep.
- 26 sporadische groepen waaronder de 5 Mathieu groepen.
Een bespreking van al die groepen vind je in de “atlas van de eindige groepen ” van Conway,Curtis,Norton,Parker en Wilson.
Koordenvierhoeken
Een koordenvierhoek is een vierhoek waarbij de vier hoekpunten op een cirkel gelegen zijn.
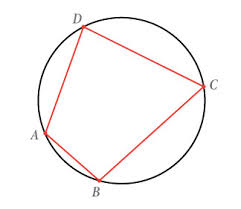Enkele eigenschappen:
- Een koordenvierhoek is altijd convex.
- Een vierhoek is een koordenvierhoek als en slechts als de overstaande hoeken supplementair zijn ( samen gelijk aan 180°).
: de stelling van Ptolemaeus.- Een vierhoek is een koordenvierhoek als en slechts als de hoek gevormd door een zijde en een diagonaal gelijk is aan de hoek gevormd door de overstaande zijde en de overstaande diagonaal.
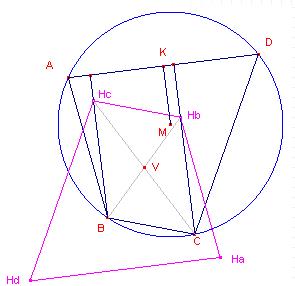
- De hoogtepunten van de vier diagonaaldriehoeken vormen een driehoek die congruent is met de gegeven vierhoek.
