Maandelijks archief: mei 2018

rekenkundig en harmonisch gemiddelde in een trapezium

Geplaatst op door

De vraag die we willen behandelen in deze tekst luidt:

Construeer het rekenkundig gemiddelde ( RG) en het harmonisch gemiddelde (HG) van de twee evenwijdige zijden van een trapezium.

  • Her RG is vrij eenvoudig: construeer het lijnstuk door de middens van de opstaande zijden. Volgens de stelling van Thales is |EF|=\frac{1}{2}(|AB|+|CD|)
  • Voor het harmonisch gemiddelde construeren we het lijnstuk, evenwijdig aan de evenwijdige zijden, door het snijpunt van de twee diagonalen van het trapezium.
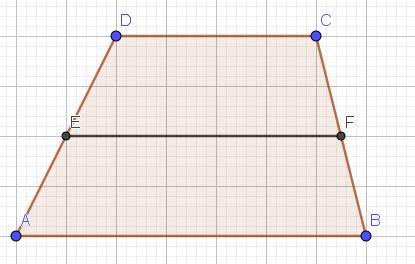
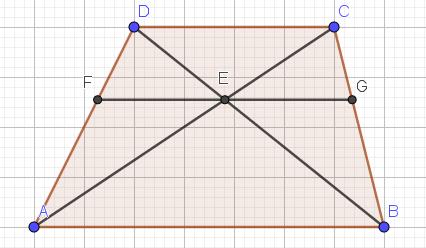    Uit de gelijkvormigheid van de driehoeken FDE en ADB, CEG en CAB, DEC en EAB volgt dat |FE|=|EG|. Construeer nu , door C, een evenwijdige aan AD. Noteer |AB|=a,|CD|=b en |FG|=x
    Nu is |EH|=b-\frac{1}{2}x en |HG|=x-b. De 3 concurrente rechten AC,IC en BC worden gesneden door 2 evenwijdige rechten, dus geldt volgens Thales dat \frac{|EH|}{|AI|}=\frac{|GH|}{|BI|} of \frac{b-\frac{1}{2}x}{b}=\frac{x-b}{a-b}. Hieruit volgt dat x=\frac{2ab}{a+b} en dit betekent dat |EF| het harmonisch gemiddelde is van de twee evenwijdige zijden van het trapezium.

 

Ongelijkheid van Cauchy-Schwarz

Geplaatst op door

Stel (a_1,a_2,\cdots,a_n) en (b_1,b_2,\cdots,b_n)  n-tallen van reële getallen, dan geldt:

(a_1b_1+a_2b_2+\cdots+a_nb_n)^2\leq(a_1^2+a_2^2+\cdots+a_n^2)(b_1^2+b_2^2+\cdots+b_n^2)

Deze ongelijkheid werd genoemd naar A.L.Cauchy( 1789-1857) en H.A.Schwarz(1843-1921) en steunt op de eigenschap dat het skalair product van twee vectoren kleiner is dan of gelijk is aan het product van de normen van die vectoren.


 

 

 

 

 

 

Bekijken we even een voorbeeld:

Bewijs: (\frac{x}{2}+\frac{y}{3}+\frac{z}{6})^2 \leq \frac{x^2}{2}+\frac{y^2}{3}+\frac{z^2}{6}

Het is enkel de kwestie van goed de twee drietallen te kiezen.
Neem (\frac{x}{2},\frac{y}{\sqrt{6}},\frac{z}{\sqrt{12}}) en  (1,\sqrt{\frac{2}{3}},\sqrt{\frac{2}{6}}) en vul in.

Nog een luciferspel

Geplaatst op door

Een willekeurig aantal lucifers is op willekeurige wijze verdeeld over twee stapels. Twee spelers nemen om de beurt lucifers weg: ofwel van één van de hopen 1,2,of 3 lucifers ofwel van beide hopen een zelfde aantal lucifers en dan ook 1,2 of 3. De speler die de laatste lucifer(s) wegneemt, wint.

We zoeken naar gunstige situaties. Met (a,b) noteren we de situatie waarbij er a lucifers op één hoop liggen en b lucifers op de andere stapel. De situaties (a,b) en (b,a) zijn identiek.

  • Met 1 lucifer hebben we enkel de situatie (1,0) en die is natuurlijk ongunstig want de tegenstrever kan gewoon die lucifer wegnemen en wint alzo het spel.
  • Met twee lucifers heb je (2,0), en (1,1) en beiden zijn ongunstig .
  • Met 3 lucifers heb je (3,0) en (2,1). De eerste situatie is zeker ongunstig maar (1,2) of (2,1) is wel degelijk gunstig, want wat de tegenstrever ook doet, hij komt terecht in een ongunstige toestand.
  • De situaties (2,2)  en (3,1) zijn ongunstig. Bij de eerste situatie kan de tegenstrever gewoon alles wegnemen en in het tweede geval kan hij door 1 lucifer weg te nemen terechtkomen in de winnende positie (2,1). Verder  is (4,0) uiteraard gunstig.

De situaties (4k,4l) en (4k+1,4l+2) zijn altijd gunstig. De winnende strategie bestaat erin elke gegeven spelsituatie om te zetten in een gunstige situatie. In sommige spelsituaties heb je de keuze  tussen twee of zelfs drie goede zetten. Zo kan je bijvoorbeeld (8,9) omzetten in de winnende situaties (8,8) en (6,9) door respectievelijk 1 lucifer weg te nemen van de stapel met 9 lucifers ofwel door er 2 weg te nemen van de andere stapel. Kies dan nu eens de ene en dan weer de andere voortzetting om de spelstrategie minder transparant te maken voor de tegenstrever. Als de winnende spelstrategie niet kan worden uitgevoerd, bestaat de optimale strategie erin 1 lucifer weg te nemen van de hoop met het meest aantal lucifers.

De Nederlandse wiskundige W.A. Wythoff  (6 oktober 1865 – 21 mei 1939) publiceerde in 1904 een analyse van dit spel.

Scherp of stomp

Geplaatst op door

Zijn er meer scherpe dan stompe driehoeken? Tellen dan maar. Maar dan zouden er evenveel zijn, namelijk oneindig veel. Misschien moeten we de vraag anders stellen: Neem de verzameling van alle driehoeken. Wat is de kans, dat een willekeurig genomen element van die verzameling, stomp is?

De vraag is dan uiteraard hoe we de verzameling van alle driehoeken vastleggen. Omdat de grootte van de hoeken van essentieel belang is, lijkt het gunstig om met elke driehoek een koppel getallen (x,y) te laten overeenkomen. Hierbij zijn de hoeken van de driehoek dan x,y en \pi -(x+y). Om een driehoek te vormen moeten x en y voldoen aan:

\begin{cases} 0<x<\pi \\0 <y<\pi\\ 0<x+y<\pi \end{cases}

De verzameling driehoeken komt dan overeen met de driehoek ABC.

Om scherp te zijn moet x en y voldoen aan:

\begin{cases} 0<x<\frac{\pi}{2} \\0 <y<\frac{\pi}{2}\\ \pi-(x+y)<\frac{\pi}{2} \end{cases}

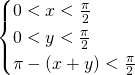
Dit komt overeen met driehoek DEF. De kans opdat een driehoek scherp zou zijn kunnen we dan berekenen door de oppervlaktes te vergelijken en dus is de kans dat een driehoek scherp is gelijk aan \frac{1}{4}. Of met andere woorden de kans dat een driehoek stomp is, is \frac{3}{4}.

Opmerkingen:

  • De punten op DE en EF geven een rechthoekige driehoek. Het is duidelijk dat de kans dat een driehoek rechthoekig is, gelijk is aan 0.
  • Er zijn ook andere mogelijkheden om de verzameling driehoeken vast te leggen. Je kan bijvoorbeeld drie punten op een cirkel nemen, waarvan je één vast houdt. Je kan dan werken met omtrekshoeken en middelpunts hoeken.