Maandelijks archief: februari 2018
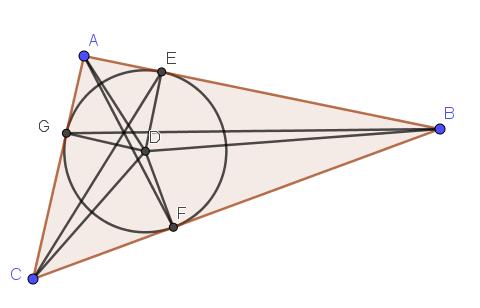
Hoektransversalen in een driehoek
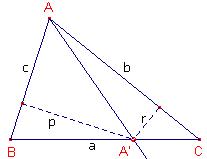
Neem een driehoek ABC. Een rechte l door een hoekpunt A van de driehoek heet hoektransversaal of ceviaan van A. We onderzoeken onder welke voorwaarden de hoektransversalen van A,B en C door één punt gaan.
- Voor een willekeurig punt P op een hoektransversaal beschouwen we de verhouding van de afstanden tot de twee zijden.
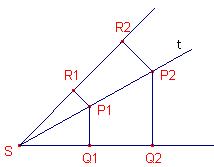 Omdat
Omdat  , is deze verhouding constant. Noem deze constante
, is deze verhouding constant. Noem deze constante  Bij elke transversaal hoort een dergelijke constante. Bereken ze met de klok mee. Nu geldt: De 3 hoektransversalen zijn concurrent als en slechts als
Bij elke transversaal hoort een dergelijke constante. Bereken ze met de klok mee. Nu geldt: De 3 hoektransversalen zijn concurrent als en slechts als 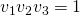 . Zo geldt bijvoorbeeld voor de binnenbissectrices van een driehoek dat
. Zo geldt bijvoorbeeld voor de binnenbissectrices van een driehoek dat  , dus: de drie binnenbissectrices van een driehoek gaan door één punt.
, dus: de drie binnenbissectrices van een driehoek gaan door één punt. - Laat men ook transversalen toe buiten de driehoek, dan moet men aan de constanten
 enkel een ander teken geven. Hetr esultaat van hierboven blijft behouden.
enkel een ander teken geven. Hetr esultaat van hierboven blijft behouden. - We kunnen een hoektransversaal ook kenmerken door de verhouding
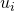 van de oppervlaktedelen waarin de driehoek door de ceviaan verdeeld wordt.
van de oppervlaktedelen waarin de driehoek door de ceviaan verdeeld wordt.
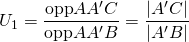 . Het is eenvoudig te zien dat
. Het is eenvoudig te zien dat 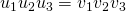 en dus geldt: De 3 hoektransversalen zijn concurrent als en slechts als
en dus geldt: De 3 hoektransversalen zijn concurrent als en slechts als  . Onder deze vorm is de stelling ook gekend als de stelling van Ceva.
. Onder deze vorm is de stelling ook gekend als de stelling van Ceva. - Nu geldt bijvoorbeeld voor de zwaartelijnen van een driehoek dat
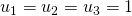 , dus: de drie zwaartelijnen van een driehoek gaan door één punt.
, dus: de drie zwaartelijnen van een driehoek gaan door één punt. - We kunnen dit ook ondzerzoeken voor de drie hooigtelijnen.
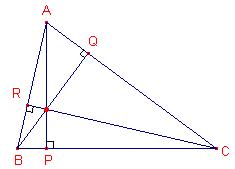
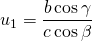 ,
,  en
en 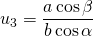 en dus is
en dus is  . Bijgevolg geldt: de drie hoogtelijnen van een driehoek gaan door één punt.
. Bijgevolg geldt: de drie hoogtelijnen van een driehoek gaan door één punt.
Cirkellimiet van Escher
 Maurits Cornelis Escher was een Nederlandse kunstenaar, die bekend is om zijn houtsneden, houtgravures en lithografieën, waarin hij vaak speelde met wiskundige principes. Geboeid door het begrip ‘oneindig’ maakte hij dit werk: de cirkel limiet. Door herhaling van eenzelfde patroon op een steeds krimpende schaal ontstaan zelfgelijkvormige figuren die een limiet karakter in zich dragen en dikwijls de vorm van een fractaal aannemen.
Maurits Cornelis Escher was een Nederlandse kunstenaar, die bekend is om zijn houtsneden, houtgravures en lithografieën, waarin hij vaak speelde met wiskundige principes. Geboeid door het begrip ‘oneindig’ maakte hij dit werk: de cirkel limiet. Door herhaling van eenzelfde patroon op een steeds krimpende schaal ontstaan zelfgelijkvormige figuren die een limiet karakter in zich dragen en dikwijls de vorm van een fractaal aannemen.
Escher schreef hierover: “Ik heb mij rot gewerkt om die litho af te maken en vervolgens de tanden op mekaar, vier dagen lang nog eens negen mooie afdrukken van die hoogst
bewerkelijke cirkellimiet-in-kleuren gemaakt. Elke druk bestaat uit een serie van
twintig maal afdrukken: vijf planken, elke plank vier keer. Dit alles met het eigenaardige gevoel dat dit werkstuk een ‘mijlpaal’ in mijn ontwikkeling betekent en dat er nooit iemand zal zijn, behalve ikzelf, die dat zal inzien.”
Inversie
We kennen de spiegeling rond een rechte als transformatie van het vlak. De dekpunten zijn de punten van de” rechte en lengte en hoeken zijn invarianten. Maar er betaat ook een spiegeling in een cirkel: de inversie. Lees in bijgevoegde tekst hoe dit tewerk gaat en hoe je die techniek kan gebruiken om bepaalde meetkundige problemen over o.a. orthogonale cirkels en rakende cirkels, eenvoudiger op te lossen.
Het begrip inversie hebben we te danken aan de Zwitserse wsikundieg Jacob Steiner ( 1796-1863). Het wiskundige werk van Steiner beperkte zich tot meetkunde. Hij behandelde dit synthetisch en geheel niet analytisch.