Wiskunde is leuk

Opgave 8

Geplaatst op 18 december 2017 door admin

Als a,b en c de maatgetallen voorstellen van de zijden van een driehoek, dan geldt

$\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}<2$

Antwoord

Omdat a,b en c de maatgetallen voorstellen van de zijden van een driehoek, weten we dat elke zijde kleiner is dan de som van de twee andere zijden. Dus bijvoorbeeld $a<b+c$
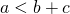
Dan is $\frac{a}{b+c}=\frac{2a}{2(b+c)}=\frac{2a}{(b+c)+(b+c)}$ .
Door toepassing van de driehoeksongelijkheid op het eerste deel van de noemer vinden we dat
$\frac{a}{b+c}<\frac{2a}{a+b+c}$

.
Op analoge wijze vinden we dat $\frac{b}{c+a}<\frac{2b}{a+b+c}$ en $\frac{c}{a+b}<\frac{2c}{a+b+c}$ .
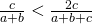Alles samenvoegen geeft
$\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}< \frac{2a+2b+2c}{a+b+c}=2$

Hoeden raadsel

Geplaatst op 16 december 2017 door admin

Drie personen A,B en C zitten in een donkere kamer. Er liggen daar ook 3 zwarte en 2 witte hoeden. Zonder ze te zien, zet iedereen één hoed op zijn hoofd. Ze gaan op een rijtje naar buiten, zodat C ziet welke hoed A en B op heeft. Persoon B ziet welke hoed A op heeft. A ziet niets. Dan zegt C: ik weet niet welke hoed ik op heb. B, die dat gehoord heeft, zegt : ik weet ook niet welke hoed ik op heb. Nu zegt A triomfantelijk: ik weet dat wel! Welke hoed heeft A op en waarom?

Antwoord

Als C niet weet welke hoed B en A op hebben, dan kunnen dit zeker geen twee witte hoeden zijn. Want anders zou hij weten dat hijzelf een zwarte hoed moest hebben.
Als A nu een witte hoed zou hebben, dan weet B dat hij zeker geen witte hoed kan hebben, want anders zouden A en B twee witte hoeden hebben, wat volgens vorig pountje niet kan.
Dus heeft A een zwarte hoed op!

Waag eens een gokje

Geplaatst op 15 december 2017 door admin

Je kan een aantal mogelijke oplossingen uitproberen. Misschien kan je zelfs het aantal mogelijke oplossingen beperken. Dan kan je best een gokje wagen en daarna proberen te bewijzen dat jouw voorstel tot oplossing de goede is.

Bepaal de volgende term in de rij:

$-1,-1,1,5,11,19,29,\cdots$

Het is zeker geen rekenkundige rij. Een eerste graadsveelterm zal dus niet kunnen om de algemene term van de rij te bepalen. Het is ook geen meetkundige rij , dus ook een exponentiële functie zal niet volstaan.
Proberen we even met een tweedegraadsfunctie. Dus een uitdrukking van de vorm $P(x)=ax^2+bx+c$ . Proberen we nu de waarden van de onbekenden $a,b$ en $c$ te vinden.
Uit $P(1)=P(2)=-1$ en $P(3)=1$ vinden we een stelsel:
$\left\{ \begin{array}{l}a+b+c=-1 \\ 4a+2b+c=-1\\9a+3b+c=1 \end{array} \right$

.
De oplossing van het stelsel is $a=1$ , $b=-3$ e, $c=1$ .
De vraag is natuurlijk of onze gok goed was! Voldoen de andere termen van de rij ook aan het voorschrift?
Nu is: $P(4)=5$ , $P(5)=11$ , $P(6)=19$ , $P(7)=29$ .
De volgende term in de rij is $P(8)=41$ .

Veralgemeen

Geplaatst op 15 december 2017 door admin

Het lijkt paradoxaal, maar soms kan een probleem vereenvoudigd en dus meer handelbaar en verstaanbaar gemaakt worden door het te veralgemenen. Een meer algemenere formulering opent soms bredere perspectieven, laat de niet essentiële zaken weg en voorziet ons soms van een nieuw arsenaal van technieken.

Wat is het grootst:

$\sqrt[3]{60} \text{ of } 2+\sqrt[3]{7}$

De derde macht nemen van beide getallen lijkt erg ingewikkeld te worden.
Probeer het meer algemeen probleem op te lossen: Wat is het grootst: $A=\sqrt[3]{4(x+y)}$ of $B=\sqrt[3]{x}+\sqrt[3]{y}$ ? Hierbij zijn $x$ en $y$ positief. De opgave is dan het speciaal geval met $x=8$ en $y=7$ .
Stel $x=a^3$ en $y=b^3$ . Dan is $B^3=(a+b)^3=a^3+3a^2b+3ab^2+b^3$ . Verder is $A^3=4(a^3+b^3)$ .
Nu is $A^3-B^3=3(a^3+b^3-a^2b-ab^2)=(a-b)(a^2-b^2)=(a-b)^2(a+b)$ . Omdat $x$ en $y$ positief zijn, zijn ook $a$ en $b$ positief en is $A^3-B^3 >0$ . Hieruit volgt dat $A^3 > B^3$ en dus ook dat $A>B$ .
We besluiten dat $\sqrt[3]{60}$ groter is dan $2+\sqrt[3]{7}$ .

Verdeel in verschillende gevallen

Geplaatst op 15 december 2017 door admin

Soms kan het probleem verdeeld worden in een aantal deelproblemen , die elk afzonderlijk kunnen behandeld worden. Dit gebeurt dikwijls als het probleem de al-kwantor bevat: voor alle x … Deze methode wordt ook wel het uitputtingsprincipe genoemd of de exhaustie methode.

Gegeven is een functie $f:\mathbb{Q} \longrightarrow \mathbb{R}$ met

$\forall x,y \in \mathbb{Q}: f(x+y)=f(x)+f(y)$

Bewijs dat $\forall x\in \mathbb{Q}: f(x)=f(1).x$ .

We gaan het resultaat eerst bewijzen voor de positieve gehele getallen. De eigenschap klopt voor x = 1.
Voor x = 2 hebben we $f(2)=f(1+1)=f(1)+f(1)=2.f(1)$ .
Voor x = 3 is $f(3)=f(2+1)=f(2)+f(1)=2.f(1)+f(1)=3.f(1)$ .
Het is duidelijk dat we dit proces kunnen verderzetten en dat voor elk positief geheel getal n geldt dat $f(n)=n.f(1)$
Nu controleren we de formule voor niet positieve gehelen. Eerst is er $f(0)=f(0+0)=f(0)+f(0)$ . Hieruit volgt dat $f(0)=0=0.f(1)$ . Neem nu het negatief getal m, dan is er een positief geheel getal n met $m=-n$ . Bijgevolg is $0=f(0)=f(n+(-n))=f(n)+f(-n)$ .
Hieruit volgt dat $f(m)= f(-n)=-f(n)=-n.f(1)=m.f(1)$ , waarmee het gestelde bewezen is.
Nu komen de omgekeerden van de gehele getallen (verschillend van 0) aan de beurt. Stel $m=\dfrac{1}{n}$ , dan geldt:
$f(1)=f(\dfrac{1}{n}+\dfrac{1}{n}+\cdots+\dfrac{1}{n})=n.f(\dfrac{1}{n})$ .
Hieruit volgt dat $f(\dfrac{1}{n})=\dfrac{1}{n}.f(1)$ of $f(m)=m.f(1)$ .
Tenslotte nemen we de rationale getallen onder de loep: $x=\dfrac{m}{n}$ .
Nu is $f(\dfrac{m}{n})=f(\dfrac{1}{n}+\dfrac{1}{n}+\cdots+\dfrac{1}{n})=m.f(\dfrac{1}{n})$ .
Dus is $f(\dfrac{m}{n})=m.f(\dfrac{1}{n})=\dfrac{m}{n}.f(1)$ .
Bijgevolg geldt voor elk rationaal getal $x=\dfrac{m}{n}$ dat $f(x)=x.f(1)$ .

Als a,b en c de maatgetallen voorstellen van de zijden van een driehoek, dan geldt

Antwoord

Antwoord

Bepaal de volgende term in de rij:

Wat is het grootst:

Gegeven is een functie met Bewijs dat .

Als a,b en c de maatgetallen voorstellen van de zijden van een driehoek, dan geldt

$\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}<2$

Bepaal de volgende term in de rij:

$-1,-1,1,5,11,19,29,\cdots$

Wat is het grootst:

$\sqrt[3]{60} \text{ of } 2+\sqrt[3]{7}$

Gegeven is een functie $f:\mathbb{Q} \longrightarrow \mathbb{R}$ met

$\forall x,y \in \mathbb{Q}: f(x+y)=f(x)+f(y)$

Bewijs dat $\forall x\in \mathbb{Q}: f(x)=f(1).x$ .