De Franse wiskundige Henri Poincaré (1854-1912) getuigt ( Mathematical Creation, in The foundations of Science):” geheel tegen mijn gewoonte dronk ik zwarte koffie en ik kon niet slapen. De ideeën kwamen bij bosjes op en ik voelde dat ze met elkaar in botsing kwamen, zodat paren van ideeën zich bij elkaar aansloten, om het zo maar eens te zeggen, tot ze een stabiele combinatie vormden. Het schijnt dat in zulke gevallen, men getuige is van het werk dat door het eigen onbewuste gedaan wordt.
De rede werkt sequentieel: stap voor stap komt men vanuit de aannamen tot nieuwe
uitspraken. Bij de intuïtie gaat het anders: men komt opeens tot een uitspraak en men
weet eigenlijk niet hoe. Intuïtie vormt een belangrijk element bij de beoefening van de
wiskunde .
Een uitspraak verkregen via de intuïtie kan een belangrijke schakel vormen in een complex bewijs of begrip. Deze intuïtieve stap moet nog wel gecontroleerd worden. In een uiteindelijk opgeschreven bewijs ziet men dan vaak niet meer terug of een stap op grond van redeneren of op grond van intuïtie gezet is.
Voor de Duitse wiskundige Gauss (1777-1855) kwam de grote intuïtie van God. De
Franse wiskundigen Poincaré (1854-1912) en Hadamard (1865-1962) hebben uitgebreid over dit onderwerp geschreven. Poincaré stelt dat intuïtie ontstaat
doordat het onbewuste voortdurend met de materie bezig is. De wiskundige schoonheidsbeleving speelt hierbij een belangrijke rol, doordat het onderbewustzijn het
bewuste denken ‘wakker maakt’ wanneer er een wiskundige ontdekking gedaan is.
Meestal gaan deze gepaard met een grote schoonheidsbelevenis. Daarna moet de intuïtie wel op haar juistheid geverifieerd worden. Een andere Franse wiskundige, Hadamard (1865-1963) stelt dat het onbewust denken niet volgens lukraak toeval verloopt, maar volgens bepaalde patronen. Hiervoor is wel de juiste geestelijke voorbereiding nodig. Dan maakt de geest in eerste instantievele combinaties waaruit in tweede instantie de juiste gekozen worden.



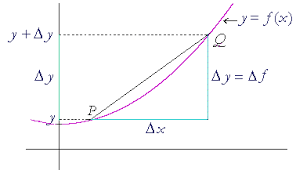
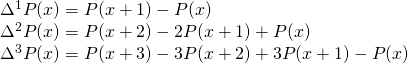
![Rendered by QuickLaTeX.com \[a_n.n!=\Delta^nP(x)= \sum_{k=0}^n(-1)^k\binom{n}{k}P(x+n-k)\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-ab065617069a871c609379661431790a_l3.png?media=1678572382)
![Rendered by QuickLaTeX.com \[a_n.n!= \sum_{k=0}^n(-1)^k\binom{n}{k}P(x-k)\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-ffeba57122f70dedd2bfaf9c3672370c_l3.png?media=1678572382)
![Rendered by QuickLaTeX.com \[a_n.n!= \sum_{k=0}^n(-1)^{n-k}\binom{n}{k}P(x+k)\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-edafc41b31f67049cf60c965dba87cc5_l3.png?media=1678572382)
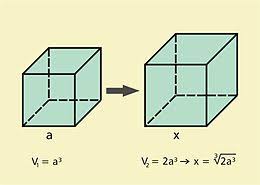
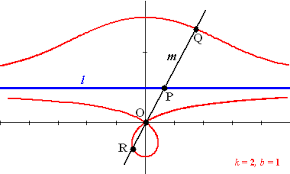

![Rendered by QuickLaTeX.com \[\begin{array}{c|c|c} n&k+1&\text{huisnummer}\\ \hline \\ 1&1&2\\8&6&12\\49&35&70\\288&204&408 \end{array}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-36ec7d05503c33ffb4c37d4fc34cf7a5_l3.png?media=1678572382)
