Maandelijks archief: februari 2017

Wie honderd zegt wint!

Geplaatst op door

Twee spelers zijn in competitie. De eerste speler A noemt een natuurlijk getal tussen 0 en 12 ( dus 1,2,…of 11). De tweede speler B telt er een getal tussen 0 en 12 bij op. Dan is het weer de beurt aan A die er weer een getal tussen 0 en 12 bij optelt. De speler die als eerste, binnen die spelregels, het getal 100 bereikt is de winnaar.

Antwoord

  1. We doen aan ‘back-tracking’: we zoeken van achter naar voren naar de winstposities.
  2. Wie 99 zegt verliest, want de andere speler doet er 1 bij en eindigt zo als eerste bij 100. Dus 99 is een verliespositie.
  3. Zo zijn 98,97,…89 ook allemaal verliesposities.
  4. Maar 88 is een winstpositie, want de volgende speler moet er een getal bij optellen uit {1,2,…,11}. Hij/zij kan nooit de 100 bereiken, maar als jij de terug aan beurt wel, kan je dat altijd. Niet toevallig is 88 = 100 – 12
  5. Zet je dit idee verder, dan zijn uiteraard ook 76,64,52,40,28,16,4 allemaal winstposities.
  6. Wie het spel begrepen heeft en eerst 4 ( of een andere winstpositie ) zegt wint het spel. Je moet, na de beurt van de tegenstrever, er voor zorgen dat je terug op een volgende winstpositie terecht komt.

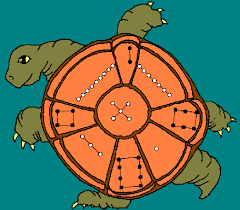
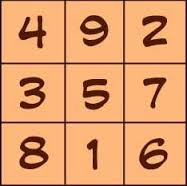
Het tovervierkant van Lo Shu

Geplaatst op door

Een tovervierkant is een vierkantig rooster van getallen zodat de som van de elementen op elke rij, kolom en diagonaal hetzelfde is. Het oudste tovervierkant wordt toegeschreven aan Lo Shu en dateert van omstreeks 2200 voor onze tijdrekening. Hij was gekerfd in het schild van een schildpad in de Lo-rovier.

Of in matrixvorm :

Als we deze matrix L noemen , kunnen we ook L² en L³ uitrekenen:

    \[L^2 =\begin{pmatrix} 59&83&83\\83&59&83\\83&83&59\end{pmatrix}\]

    \[L^3=\begin{pmatrix}1149&1029&1197\\1173&1125&1077\\1053&1221&1101\end{pmatrix}\]

De matrix L^2 is symmetrisch en is een pseudo-tovervierkant ( de som van de elementen op elke rij en in elke kolom is dezelfde; de sommen van de diagonalen echter niet ).

De matrix L^3 is dan weer wel een tovervierkant, maar de symmetrie is verdwenen.

Noorse wiskunde olympiade

Geplaatst op door

De Noorse Mathematical Society werd opgericht in 1918, en het was hier dat het idee van een jaarlijkse wiskundige competitie voor het eerst opdook. De wedstrijd werd voor de eerste keer gehouden  in 1921, en werd jaarlijks gehouden tot het midden van 1970. Kroonprins Olav, en later kroonprins Harald gaven aan de winnaars de “prijs van de kroonprins” . Het aantal deelnemers was zeer laag en soms waren er zelfs geen deelnemers, zodat de competitie tenslotte in het midden van de jaren 70 verdween.

Het duurde echter niet lang totdat men gesprekken opstartte voor een nieuwe wedstrijd. In 1979-80, op de 150ste verjaardag van de dood van Niels Henrik Abels , werd een wedstrijd gehouden voor  middelbare scholieren. Er waren 28 deelnemers. In 1981 werd de Abel wedstrijd opgestart, als een samenwerkingsverband tussen de Noorse Mathematical Society en Aftenposten (een krant). Er waren 65 deelnemers in het eerste jaar, maar dit viel zo dramatisch  terug in de volgende drie jaar dat men moest uitkijken naar een andere werkvorm.

In 1985 werd de wedstrijd omgeschakeld naar een massa-evenement : een 100-minuten beginronde die lokaal gehouden werd op de scholen, gevolgd door een finale met ongeveer 20 top studenten, en een uitnodiging aan de IMO voor de zes beste. Het aantal deelnemers is gestaag toegenomen, en bereikte in 1994 voor het eerst de kaap van de 4000.  In het najaar van 1994 werd een wijziging aangebracht: er kwamen twee rondes in de scholen vooraleer de finale kon bereikt worden. De competitie kreeg de naam: de Niels Henrik Abel Contest, en is de Noorse versie van de wiskunde olympiade. Meer info, met onder andere vragen en oplossingen van de verschillende jaargangen vind je op hun website.

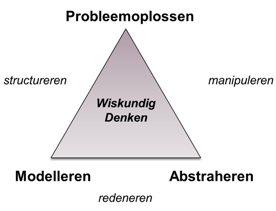
Wiskundig denken

Geplaatst op door
Wiskundig denken is de kern en de kracht van wiskunde

 

Wat is nu dat wiskundig  denken? De Nederlandse wiskundige P.Drijvers geeft volgende omschrijving:

Bedenken hoe je  wiskundig gereedschap kan gebruiken om een probleem op te lossen.

  • Hoe? : hier bedoelen we de keuze van de gereedschappen die je gaat gebruiken, in welke volgorde je dat doet en onder welke voorwaarden ze zinvol kunnen gebruikt worden.
  • Wiskundig gereedschap? : dit moet breed worden opgevat. het kan heel specifiek en concreet zijn, zoals de formule van Pythagoras, maar ook theoretisch ( logisch redeneren, bewijzen), of algemeen van karakter ( het ontwikkelen van strategieën).
  • Gebruiken? : niet allen het toepassen van een bestaande, kant-en-klare methode, maar ook het ontwikkelen ervan, of het op maat maken van een bestaande methode voor een specifiek doel.
  • Probleem? : dit is niet zomaar een opgave, maar wel een vraag waar je geen kant-en-klare oplosmethode ter beschikking hebt

 

Je kan drie kernaspecten beschouwen: probleemoplossen, modelleren en abstraheren.

Wat voor iemand een probleem is, dus wat niet standaard is voor hem of haar, hangt af van voorkennis en ervaring. Wiskundig denken is dus relatief: wat voor de ene uitdagend en nieuw is, zal voor de andere routinematige reproductie zijn.