Absolute waarde
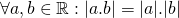
We geven eerst de definitie : en . Uit deze definitie leid je onmiddellijk af dat en . Andere eigenschappen: (driehoeksongelijkheid) De grafiek van de functie wordt gegeven door:
Maand: januari 2017
Rangeerproblemen
Een man beschikt over een klein roeibootje. Hij moet een wolf, een schaap en een kool naar de andere oever overbrengen. In het bootje is maar plaats voor de man en ofwel de wolf, ofwel het schaap, ofwel de kool. Hij mag echter de wolf en het schaap nooit alleen laten (je kan wel raden … Lees verder
Oneindige afdaling
Een bewijs door oneindige afdaling is een manier van bewijzen die kan worden toegepast bij aftelbare welgeordende verzamelingen, meestal de natuurlijke getallen. Men bewijst het niet bestaan van een element uit een verzameling met een bepaalde eigenschap, door aan te tonen dat als er zo een element zou bestaan, er ook een kleiner element moet … Lees verder
Erlanger Programm van Felix Klein
Felix Christian Klein (Düsseldorf, 25 april 1849 – Göttingen, 22 juni 1925) was een Duits wiskundige. Klein was hoogleraar aan de universiteiten van Erlangen, München, Leipzig en uiteindelijk Göttingen waar hij wiskunde doceerde. Zijn hoofdonderwerpen waren niet-euclidische meetkunde, groepentheorie en functietheorie. Naar hem is onder andere de fles van Klein genoemd. In 1912 kreeg hij de … Lees verder
Wat is het grootst: a^b of b^a?
We zien onmiddellijk dat , dat en dat . Maar kan je zonder rekentoestel bepalen of kleiner of groter is dan ? Lees het onderzoek hierover in volgende tekst.