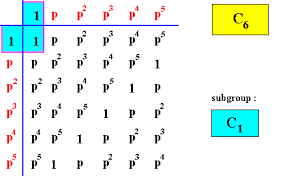
De getaltheorie houdt zich bezig met het onderzoek van eigenschappen van gehele getallen, en meer in het bijzonder , van natuurlijke getallen. In de getaltheorie is het gebruikelijk onder de verzameling van de natuurlijke getallen te verstaan de verzameling ![]() , 0 wordt dan dus niet tot
, 0 wordt dan dus niet tot ![]() gerekend.
gerekend.
Een getal ![]() is een deler van
is een deler van ![]() als er een geheel getal
als er een geheel getal ![]() bestaat waarvoor geldt dat
bestaat waarvoor geldt dat ![]() . We noteren
. We noteren ![]() . We noemen
. We noemen ![]() dan een veelvoud van
dan een veelvoud van ![]() .
.
Bij elk tweetal natuurlijke getallen ![]() en
en ![]() bestaan er gehele getallen
bestaan er gehele getallen ![]() ( voor quotiënt ) en
( voor quotiënt ) en ![]() ( voor rest ) zo , dat
( voor rest ) zo , dat
![]()
Een natuurlijk getal, groter dan 1, dat geen delers heeft buiten 1 en zichzelf noemt men een priemgetal. Een getal, groter dan 1, dat geen priemgetal is heet een samengesteld getal. Het getal 1 is dus per definitie noch priem noch samengesteld.
Een paar eigenschappen :
- Elke deler van
 en
en  deelt ook elke lineaire combinatie (
deelt ook elke lineaire combinatie (  ) van
) van  en
en  .
. - Er zijn oneindig veel priemgetallen.
- Als
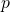 een priemgetal is dat
een priemgetal is dat  deelt, dan deelt
deelt, dan deelt 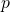 ofwel
ofwel  ofwel
ofwel  .
.